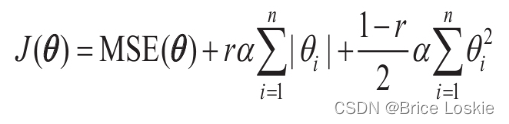岭回归、Lasso回归和弹性网络
减少过拟合的一个好方法是对模型进行正则化(即约束模型):它拥有的自由度越少,则过拟合数据的难度就越大。正则化多项式模型的一种简单方法是减少多项式的次数。
对于线性模型,正则化通常是通过约束模型的权重来实现的。现在,我们看一下岭回归、Lasso回归和弹性网络,它们实现了三种限制权重的方法
1.岭回归
岭回归(也称为Tikhonov正则化)是线性回归的正则化版本:将等于的正则化项添加到成本函数。这迫使学习算法不仅拟合数据,而且还使模型权重尽可能小。注意仅在训练期间将正则化项添加到成本函数中。训练完模型后,你要使用非正则化的性能度量来评估模型的性能。
训练过程中使用的成本函数与用于测试的性能指标不同是很常见的。除正则化外,它们可能不同的另一个原因是好的训练成本函数应该具有对优化友好的导数,而用于测试的性能指标应尽可能接近最终目标。例如,通常使用成本函数(例如对数损失(稍后讨论))来训练分类器,但使用精度/召回率对其进行评估。
超参数α控制要对模型进行正则化的程度。如果α=0,则岭回归仅是线性回归。如果α非常大,则所有权重最终都非常接近于零,结果是一条经过数据均值的平线。公式4-8给出了岭回归成本函数
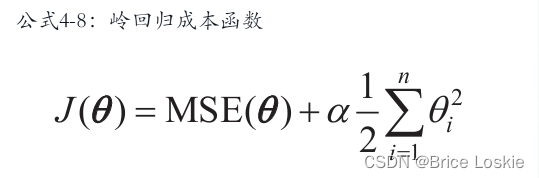
请注意,偏置项没有进行正则化(总和从i=1开始,而不是0)。如果我们将w定义为特征权重的向量
至
,则正则项等于
,其中||w||2表示权重向量的[插图]2范数[2],其中
表示权重向量的
范数。对于梯度下降,只需将αw添加到MSE梯度向量
在执行岭回归之前缩放数据(例如使用StandardScaler)很重要,因为它对输入特征的缩放敏感。大多数正则化模型都需要如此。
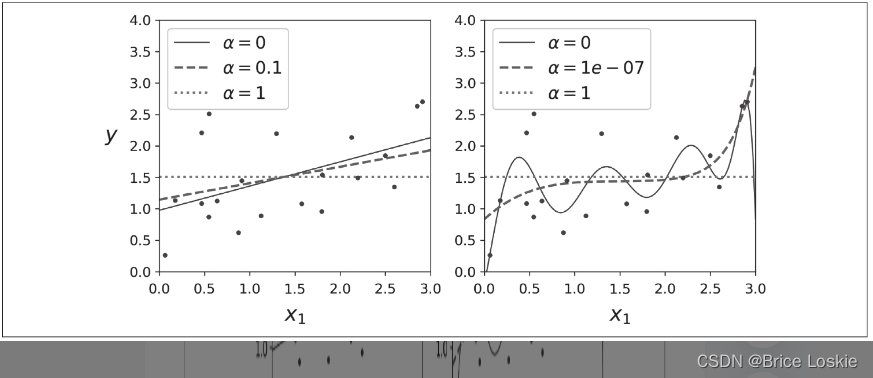
图显示了使用不同的α值对某些线性数据进行训练的几种岭模型。左侧使用普通岭模型,导致了线性预测。在右侧,首先使用PolynomialFeatures(degree=10)扩展数据,然后使用StandardScaler对其进行缩放,最后将岭模型应用于结果特征:这是带有岭正则化的多项式回归。请注意,α的增加会导致更平坦(即不极端,更合理)的预测,从而减少了模型的方差,但增加了其偏差。
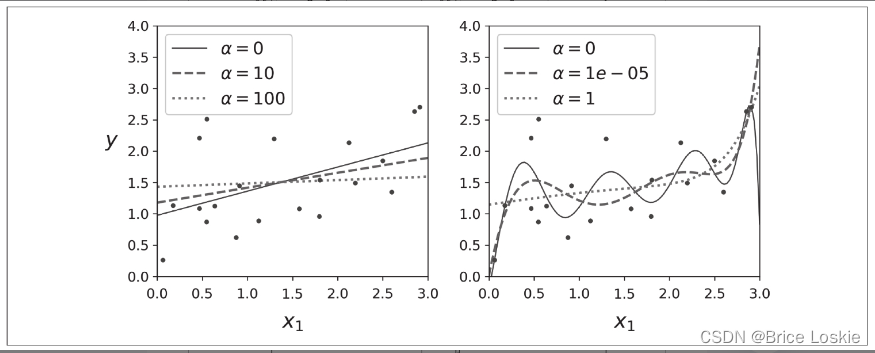
与线性回归一样,我们可以通过计算闭合形式的方程或执行梯度下降来执行岭回归。利弊是相同的。公式4-9显示了闭式解,其中A是(n+1)×(n+1)单位矩阵[3],除了在左上角的单元格中有0(对应于偏置项)。
闭式解的岭回归
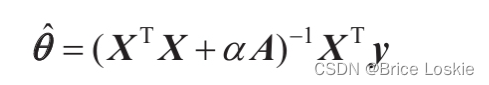
2.Lasso回归
线性回归的另一种正则化叫作最小绝对收缩和选择算子回归(Least Absolute Shrinkage and Selection Operator Regression,简称Lasso回归)。与岭回归一样,它也是向成本函数添加一个正则项,但是它增加的是权重向量的[插图]1范数,而不是[插图]2范数的平方的一半。
显示了与上图相同的东西,但是用Lasso模型替换了岭模型,并使用了较小的α值。
Lasso回归的一个重要特点是它倾向于完全消除掉最不重要特征的权重(也就是将它们设置为零的右图中的虚线(α=10-7)看起来像是二次的,快要接近于线性:因为所有高阶多项式的特征权重都等于零。换句话说,Lasso回归会自动执行特征选择并输出一个稀疏模型(即只有很少的特征有非零权重)。在左上图中,轮廓线代表[插图]1损失(|θ1|+|θ2|),当你靠近任何轴时,该损失呈线性下降。例如,如果将模型参数初始化为θ1=2和θ1=0.5,运行梯度下降会使两个参数均等地递减(如黄色虚线所示)。
3.弹性网络
弹性网络是介于岭回归和Lasso回归之间的中间地带。正则项是岭和Lasso正则项的简单混合,你可以控制混合比r。当r=0时,弹性网络等效于岭回归,而当r=1时,弹性网络等效于Lasso回归。