在一些高功率密度的应用场景中，追求极致的电压利用率，这个时候要用到过调制技术；当svpwm工作在过调制区域时，逆变电桥会在一个基波周期内多次达到100%占空比，且较多时间处于较高的占空比，这个时候下桥臂电流采样方案无法采样电流，电流重构技术用于该场景下重构无法采样的电流信号。

1、过调制

1.1、svpwm调制

此处讨论过调制相关内容默认读者熟悉svpwm调制相关理论，不熟悉的读者可以通过以下连接了解。

永磁同步电机控制笔记：扇区法svpwm实现及分析

永磁同步电机控制笔记：中点平移法svpwm实现分析

1.2、逆变器输出电压范围

对于三相逆变电桥，能够输出的电压范围如下图。
图中，V4、V2、V1方向对应U、V、W轴方向。U、V、W三轴的输出电压任意组合，其合成矢量可以落在六边形内的任意区域。其中六边形的边长为23Vdc\frac{2}{3}V_{dc}32​Vdc​，六边形的内接圆半径为33Vdc\frac{\sqrt3}{3}V_{dc}33​​Vdc​；

当svpwm调制的目标电压矢量幅度小于等于33Vdc\frac{\sqrt3}{3}V_{dc}33​​Vdc​时，期望输出在上述内接圆内或圆上，轨迹为半径等于α2+β2\sqrt{{\alpha}^2 + {\beta}^2}α2+β2​，逆变电桥能够输出完整的正弦波；

当svpwm调制的目标电压矢量幅度大于33Vdc\frac{\sqrt3}{3}V_{dc}33​​Vdc​时，期望输出在上述内接圆外，轨迹为半径大于上述内接圆半径的圆，受逆变器的允许输出范围限制，实际输出被限幅，此时进入过调制区域。

特别的，当svpwm调制的目标电压矢量幅度等于33Vdc\frac{\sqrt3}{3}V_{dc}33​​Vdc​时，输出电压在上图中的轨迹为上述六边形的内接圆，此时输出线电压的幅度等于母线电压，电压利用率达到100%.

1.3、过调制代码实现

过调制技术虽然说起来有比较多的门道，但是实现起来格外简单，回归原理的本质，就是期望到了无法输出的范围就进行限幅，当三相输出占空比大于100%时限幅到100%，当输出占空比小于0%时，限幅到0%.

for(pwmCnt=0;pwmCnt<3;pwmCnt++)
{// compute the valuefloat_t period = (float_t)(EPWM_getTimeBasePeriod(obj->pwmHandle[pwmCnt]));float_t V_pu = -pPWMData->Vabc_pu.value[pwmCnt];      // Negativefloat_t V_sat_pu = MATH_sat(V_pu,0.5f,-0.5f);           // -0.5~0.5float_t V_sat_dc_pu = V_sat_pu + 0.5f;                 // 0~1.0int16_t pwmValue  = (int16_t)(V_sat_dc_pu * period);  //// Save current CMP value for OVMpPWMData->cmpValue[pwmCnt] = pwmValue;// write the PWM data valueEPWM_setCounterCompareValue(obj->pwmHandle[pwmCnt],EPWM_COUNTER_COMPARE_A,pwmValue);
}

ti参考代码如上。

2、电流重构

2.1、电流重构的应用场景

相比较过调制更值得讨论的是电流重构，在成本敏感的电机驱动器中常采用下桥臂电流采样方案。

下桥臂电流采样方案相比较相间采样方案有如下特点。

1. 下桥臂电流采样相比较相间采样可以大大减小差分电流信号的共模噪声。
2. 下桥臂采样到的差分电流信号的对地电压极小。
3. 下桥臂电流采样方案必须在下桥臂导通的时候才有有效电流信号。

一般来说，高共模抑制比，高耐压的差分运放非常昂贵，虽然下桥臂电流采样有采样死区(此处的采样死区指在下桥臂未导通时无法进行电流采样)，但是要比更高的成本更容易接受，何况采样死区可以通过软件算法克服。

单片机或dsp电流采样需要一定的时间，假设完成电流采样的时间为Tmin，当某一相或两相下桥臂导通时间小于Tmin时，需要进行重构；好在我们的电机负载是三相对称负载，其中任意一相电流和电流相位即可反映完整的三相电流信息，且可以证明，不存在某种时刻，三相下桥同时输出小于Tmin.

为了尽可能准确的反映电机电流，下文中把电流重构场景分为重构单相电流和重构两相电流两种情况。

2.2、重构单相电流

根据基尔霍夫电流定律，电路中任一个节点上，在任一时刻，流入节点的电流之和等于流出节点的电流之和。容易分析，在电机负载中，如果任意两相电流已知，第三相电流等于两外两相电流之和的相反数，即：

ic=−ia−ibi_c = -i_a - i_b ic​=−ia​−ib​

2.3、重构两相电流

此处论讨两种通过一相已知电流重构两相未知电流的方法，一种是根据相位直接计算，一种是根据之前的电流以及正常采样的一相电流估算的方法。

若电流相位已知，三相电流可以表示为：

ia=issin(θ)ib=issin(θ+23π)ic=issin(θ−23π)i_a = i_s sin(\theta)\\ i_b = i_s sin(\theta + \frac{2}{3}\pi)\\ i_c = i_s sin(\theta - \frac{2}{3}\pi) ia​=is​sin(θ)ib​=is​sin(θ+32​π)ic​=is​sin(θ−32​π)

由以上关系，已知其中一相电流为izi_ziz​，另外两相分别为
ix=izsin(θ−23π)sin(θ)iy=izsin(θ+23π)sin(θ)i_x = i_z \frac{sin(\theta - \frac{2}{3}\pi)}{sin(\theta)}\\ i_y = i_z \frac{sin(\theta + \frac{2}{3}\pi)}{sin(\theta)}\\ ix​=iz​sin(θ)sin(θ−32​π)​iy​=iz​sin(θ)sin(θ+32​π)​

而电流相位又是跟转子位置角相关的。

若转子位置角为θ\thetaθ，aaa相电流描述为ia=issin(ψ)i_{a} =i_s sin(\psi)ia​=is​sin(ψ)，aaa相电流相位跟转子位置角的关系可以描述如下：

ψ=θ+λ+π2=θ+atan2(iq,id)+π2\psi = \theta + \lambda + \frac{\pi}{2} = \theta + atan2(i_q,i_d)+ \frac{\pi}{2} ψ=θ+λ+2π​=θ+atan2(iq​,id​)+2π​

推导过程见我的知乎回答:同步电动机的转子位置角和电压相位角以及电流相位角的关系。

3、仿真验证

搭建仿真模型进行验证

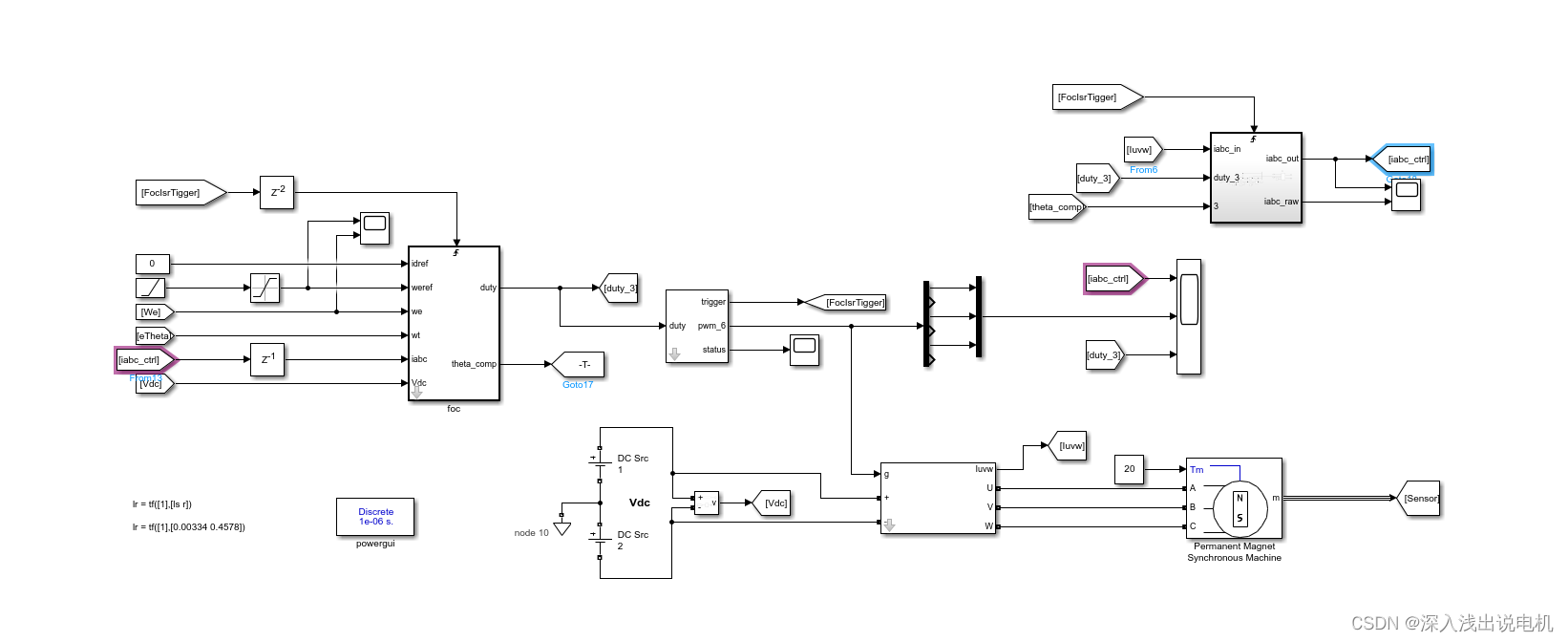
上溢事件触发电流使用速度控制，调制比给到0.6，给定速度超过电机的最大速度，使得进入最大允许调制比。

仿真中使用pwm采样以及foc运行，通过控制focTigger的时序，使得电流采样先被触发，之后执行foc程序。

为了实现下桥臂电流采样，以及控制电流采样延时，自己搭建三相逆变电桥如下：

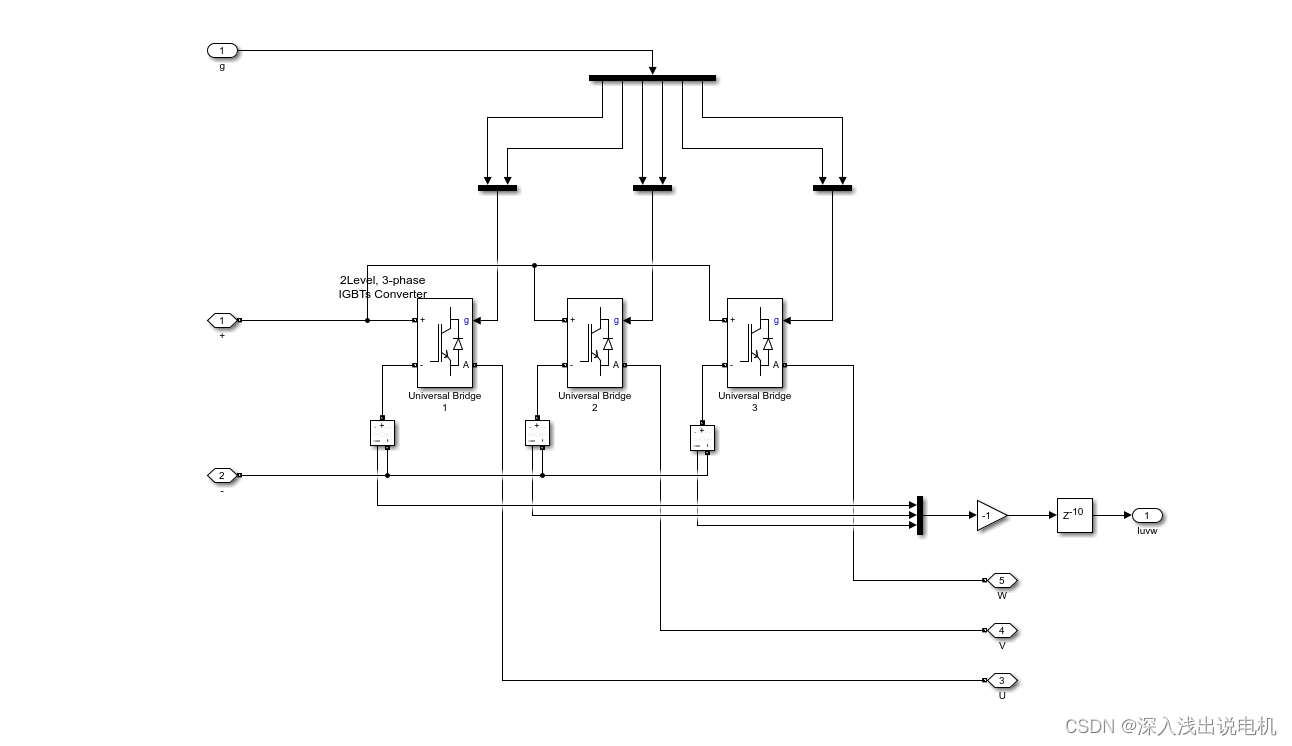
采样延时为10个系统时钟。

运行仿真。

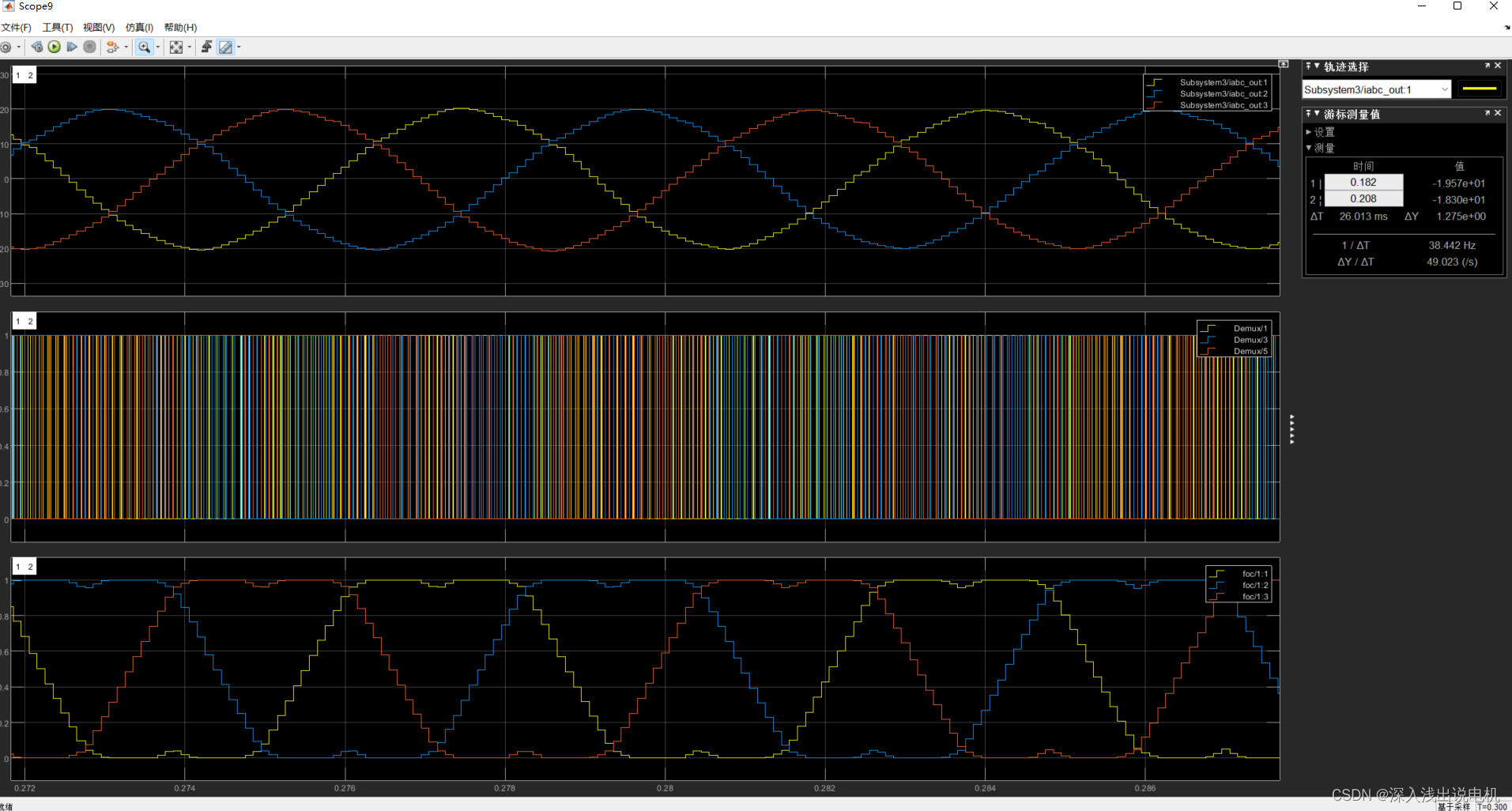
图中figure1为重构后的相电流，figure2为三路上桥臂的驱动信号，figure3为svpwm模块的输出。

可以看到高速时svpwm调制器已经进入过调制区域。输出被限幅到100%占空比，且马鞍波被部分削平，此时三相电流经过重构依然能够保持较为正弦的波形。

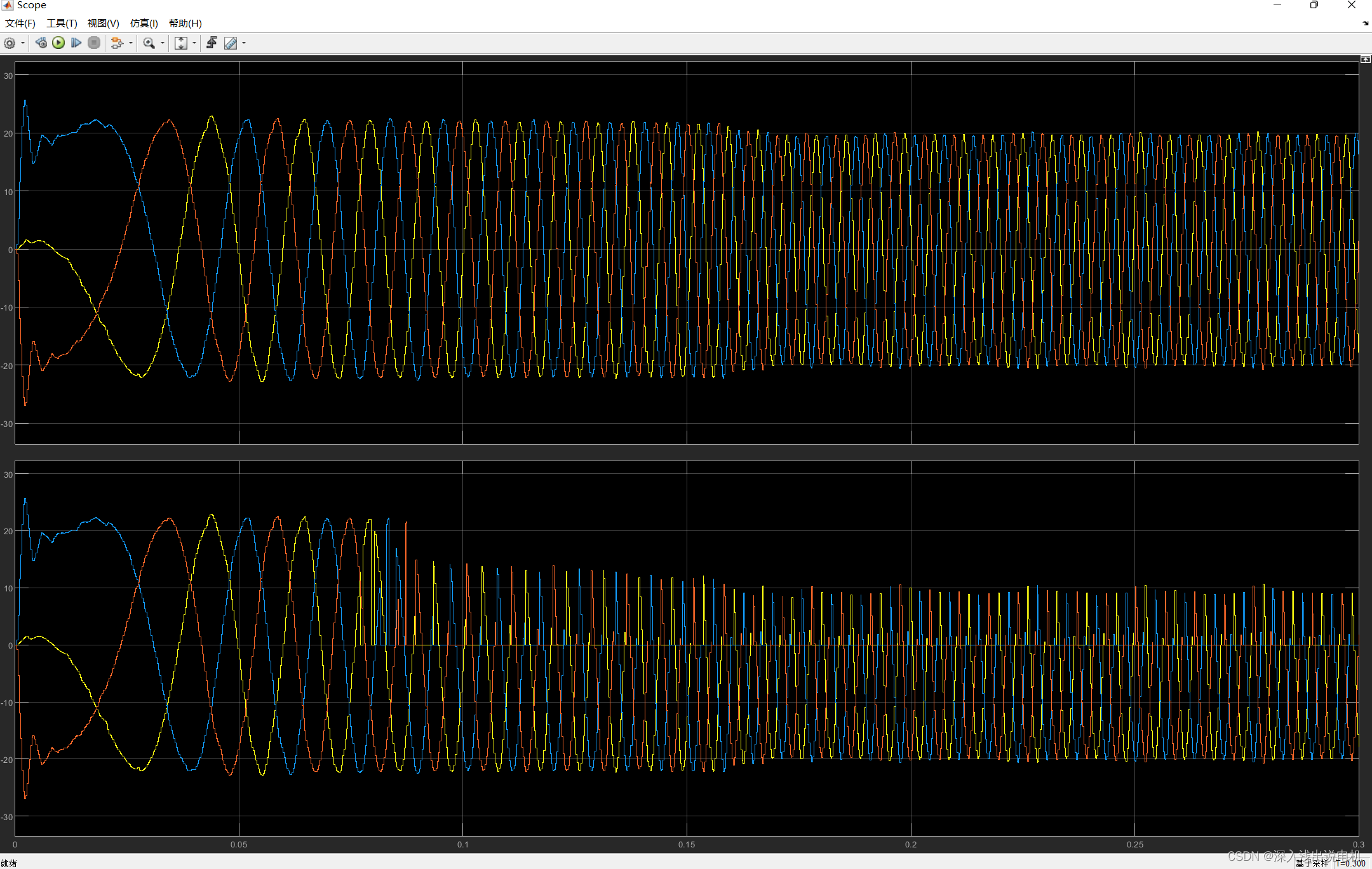
对比电流重构后的电流和采样到的原始波形。可以看到随着转速的增加，原始采样信号逐渐部分失真，转速越高失真越明显。但是经过重构的电流信号能够一直保持完整。

4、小结

本文分析过调制及电流重构，通过simulink仿真实现了过调制及电流重构，仿真的设计花费了大量的时间，希望能够对各位读者的设计起到帮助。

仿真下载方式，关注微信公众号：深入浅出说电机 回复GTZDLCG获取下载地址。