AVL树详解(附带旋转步骤图,手把手带你上分)
创始人
2024-01-20 20:58:10
0次
文章目录
- 👍 AVL树的概念先了解一下
- 😁AVL树节点的定义
- 😊AVL树插入节点
- 🤞AVL树为什么要旋转
- 😍AVL树的四种旋转
- 左单旋
- 右单旋
- 左右双旋
- 右左双旋
- ❤️结语
关于AVL树的讲解
👍 AVL树的概念先了解一下
- 它的左右子树都是AVL树
- 左右子树高度之差(简称平衡因子)的
绝对值不超过1 (-1/0/1)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-MlyXcMxn-1668154168392)(https://p6-juejin.byteimg.com/tos-cn-i-k3u1fbpfcp/6905b990ac694ebab9a03d2a44f0c8a7~tplv-k3u1fbpfcp-watermark.image?)]](/webdata/wwwroot/pics.8red.cn/weishitang/202401/81bf9f7d031edb2.png)
- 如果一棵二叉搜索树是高度平衡的,它就是AVL树。如果它有n个结点,其高度可保持在 O(log2n)O(log_2 n)O(log2n),搜索时间复杂度O(log2nlog_2 nlog2n)。
😁AVL树节点的定义
//AVL 树的节点
template
struct AVLTreeNode
{pair _kv;AVLTreeNode* _left;AVLTreeNode* _right;AVLTreeNode* _parent;//左右子数的高度差int _bf;AVLTreeNode(const pair& kv):_kv(kv),_left(nullptr),_right(nullptr),_parent(nullptr), _bf(0){}
};
😊AVL树插入节点
bool Insert(const pair& kv){// 1、搜索树的规则插入// 2、看是否违反平衡规则,如果违反就需要处理:旋转if (_root == nullptr){_root = new Node(kv);_root->_bf = 0;return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);if (parent->_kv.first < kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;// ...// 更新平衡因子while (parent) // 最远要更新根{if (cur == parent->_right){parent->_bf++;}else{parent->_bf--;}// 是否继续更新?if (parent->_bf == 0) // 1 or -1 -》 0 插入节点填上矮的那边{// 高度不变,更新结束break;}else if (parent->_bf == 1 || parent->_bf == -1)// 0 -》 1 或 -1 插入节点导致一边变高了{// 子树的高度变了,继续更新祖先cur = cur->_parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2)// -1 or 1 -》 2 或 -2 插入节点导致本来高一边又变高了{// 子树不平衡 -- 需要旋转处理if (parent->_bf == 2 && cur->_bf == 1) // 左单旋{RotateL(parent);}else if (parent->_bf == -2 && cur->_bf == -1) // 右单旋{RotateR(parent);}else if (parent->_bf == -2 && cur->_bf == 1) // 左右双旋{RotateLR(parent);}else if (parent->_bf == 2 && cur->_bf == -1) // 右左双旋{RotateRL(parent);}break;}else{// 插入之前AVL就存在不平衡子树,|平衡因子| >= 2的节点assert(false);}}return true;}
🤞AVL树为什么要旋转
当一个树左右高度差绝对值大于1 的时候就要进行旋转
这是一个简单的示范:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-fmbnuLF2-1668154168393)(https://p9-juejin.byteimg.com/tos-cn-i-k3u1fbpfcp/c39f842b8f704cccba14a58aa95ab270~tplv-k3u1fbpfcp-watermark.image?)]](/webdata/wwwroot/pics.8red.cn/weishitang/202401/39a2f19127b36c6.png)
😍AVL树的四种旋转
左单旋
图片演示(我自己纯手画):
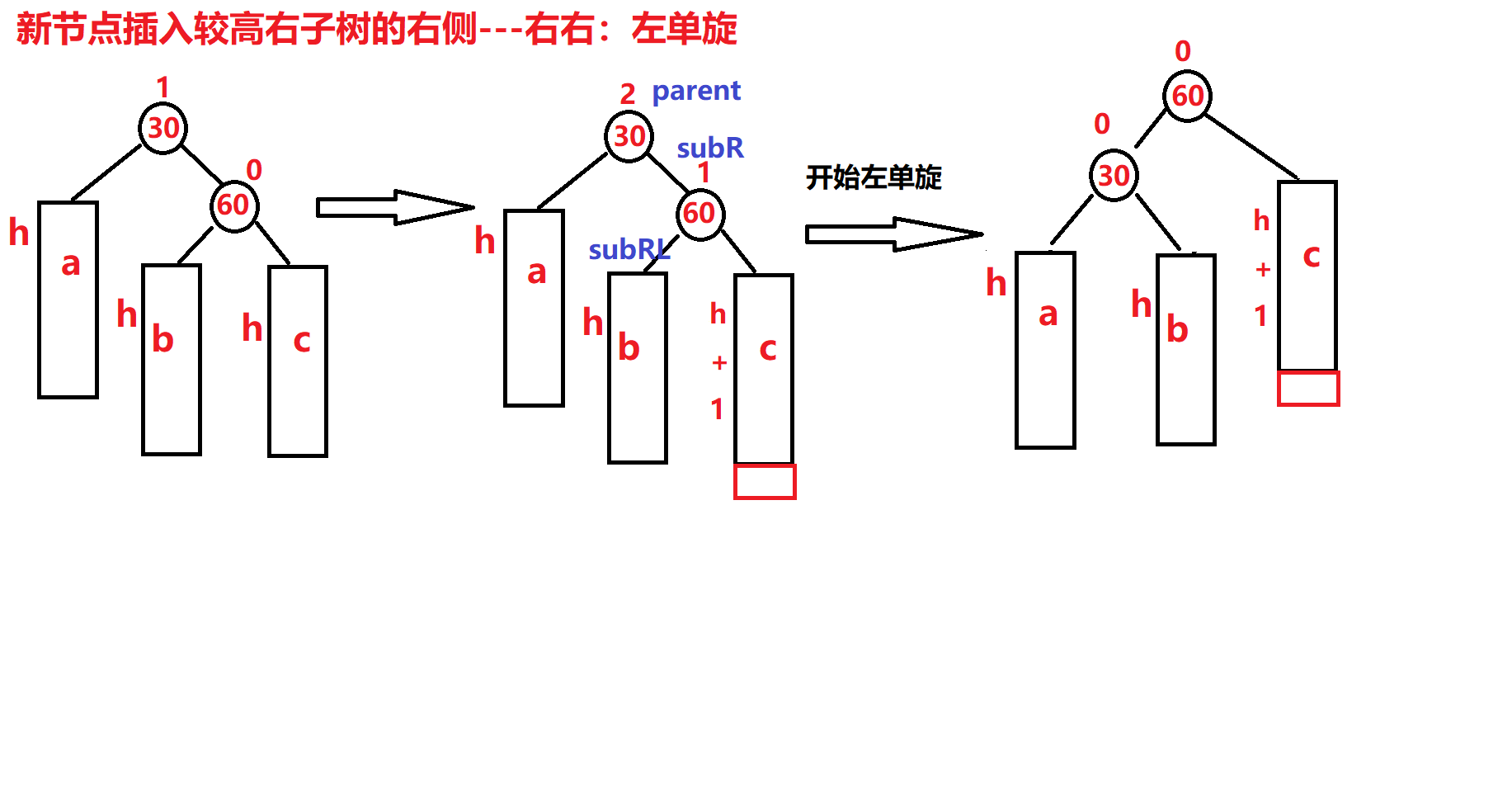
代码:
void RotateL(Node* parent)//左单旋{Node* SubR = parent->_right;Node* SubRL = SubR->_left;parent->_right = SubRL;if (SubRL){SubRL->_parent = parent;}Node* ppNode = parent->_parent;SubR->_left = parent;parent->_parent = SubR;if (_root == parent){_root = SubR;_root->_parent = nullptr;}else{if (ppNode->_left == parent){ppNode->_left = SubR;}else{ppNode->_right = SubR;}SubR->_parent = ppNode;}//旋转结束更新平衡因子parent->_bf = 0;SubR->_bf = 0;}右单旋
图片演示(我纯手画)
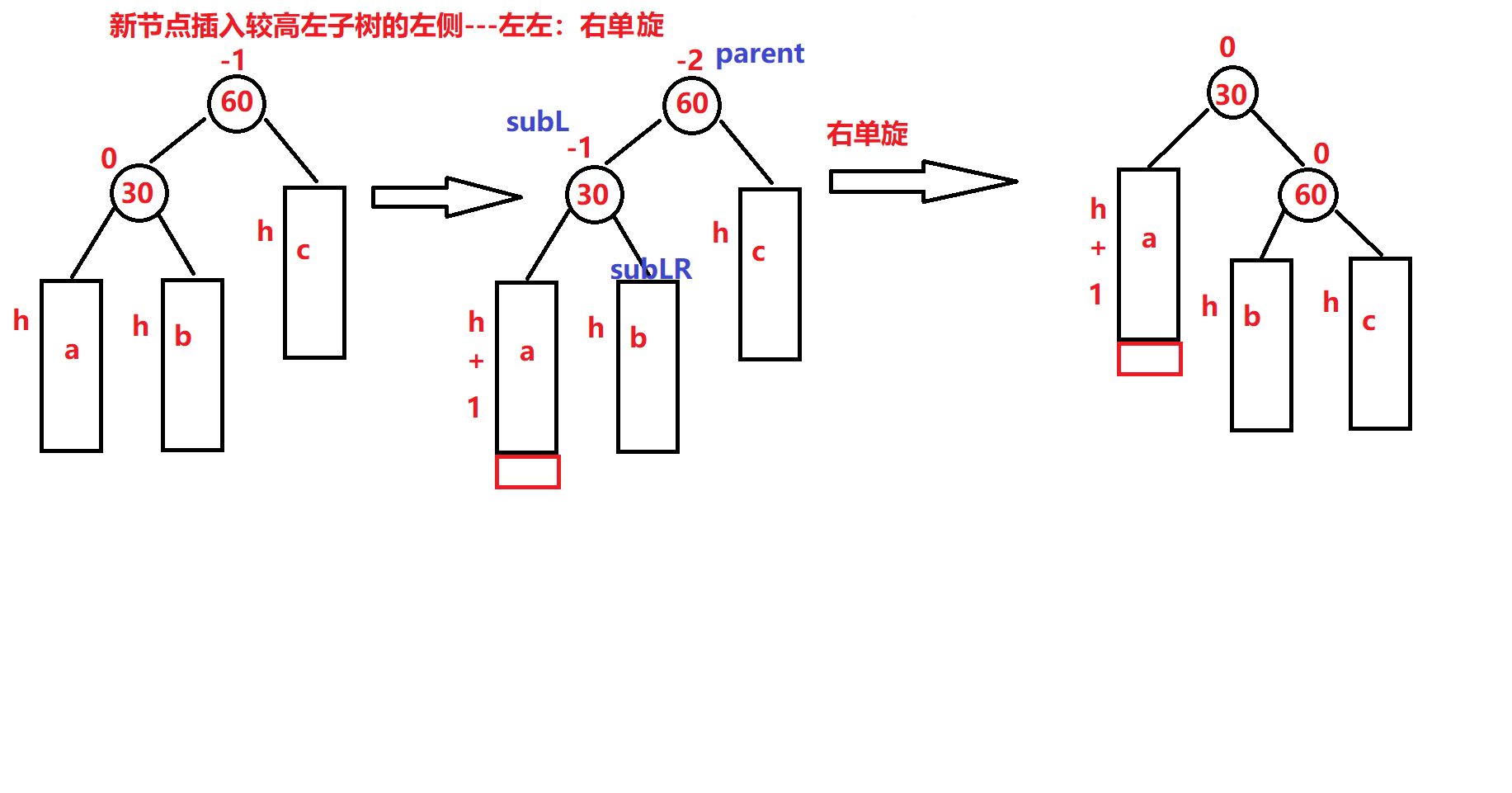
代码:
void RotateR(Node* parent)//右单旋{Node* SubL = parent->_left;Node* SubLR = SubL->_right;parent->_left = SubLR;if (SubLR){SubLR->_parent = parent;}Node* ppNode = parent->_parent;SubL->_right = parent;parent->_parent = SubL;if (_root == parent){_root = SubL;_root->_parent = nullptr;}else{if (ppNode->_left == parent){ppNode->_left = SubL;}else{ppNode->_right = SubL;}SubL->_parent = ppNode;}//旋转结束更新平衡因子parent->_bf = 0;SubL->_bf = 0;}
左右双旋
图片演示(我纯手画):
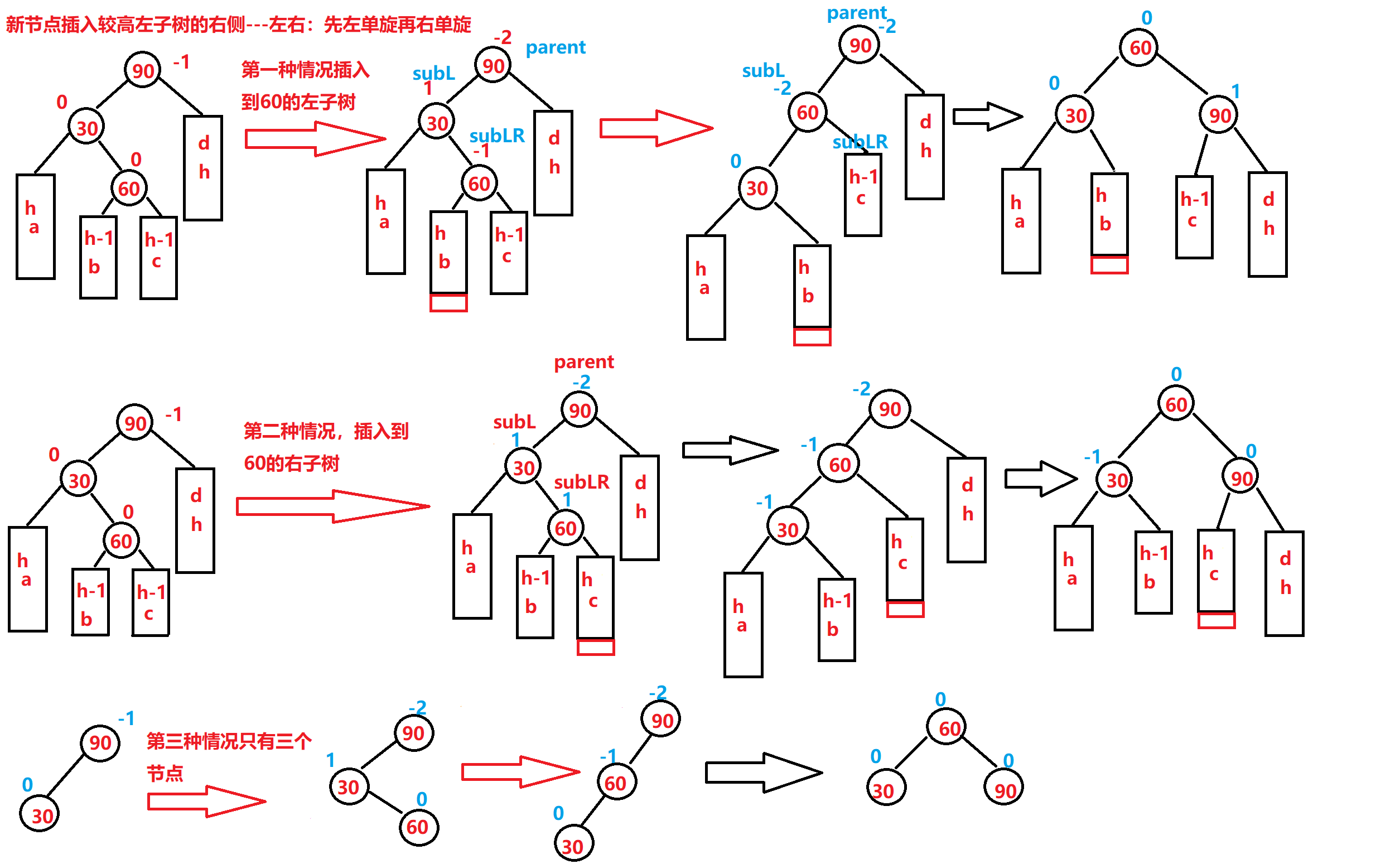
parent节点平衡因子和subL节点的平衡因子都与subLR有关
| subLR | parent | subL |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | -1 |
| -1 | 1 | 0 |
代码:
void RotateLR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;RotateL(parent->_left);RotateR(parent);// 更新平衡因子if (bf == 0){parent->_bf = 0;subL->_bf = 0;subLR->_bf = 0;}else if (bf == 1){parent->_bf = 0;subL->_bf = -1;subLR->_bf = 0;}else if (bf == -1){parent->_bf = 1;subL->_bf = 0;subLR->_bf = 0;}else{// subLR->_bf旋转前就有问题assert(false);}}右左双旋
图片演示(我自己纯手画):
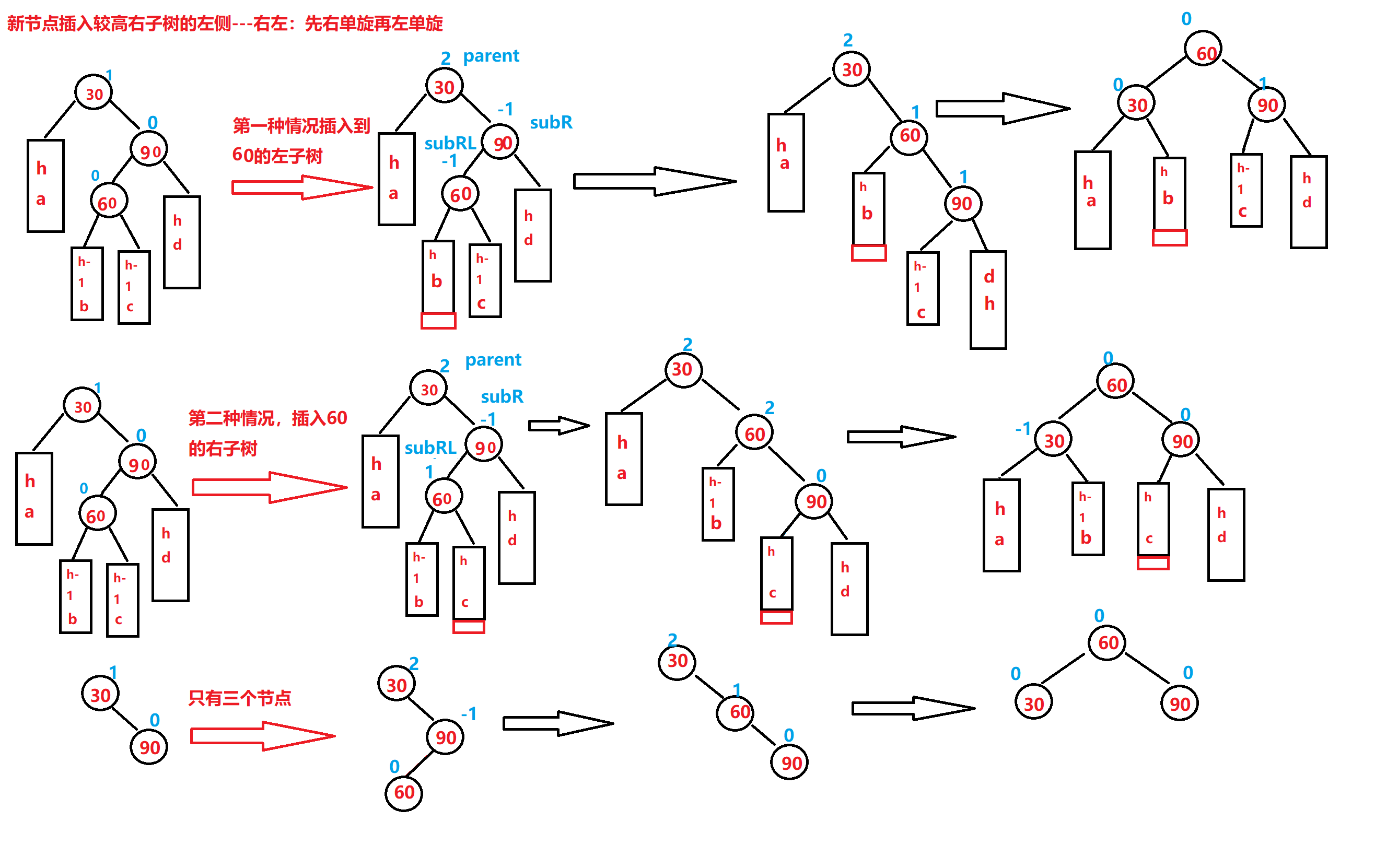
e?)]
parent节点平衡因子和subR节点的平衡因子都与subRL有关
| subRL | parent | subR |
|---|---|---|
| 0 | 0 | 0 |
| 1 | -1 | 0 |
| -1 | 0 | 1 |
代码:
void RotateRL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RotateR(parent->_right);RotateL(parent);if (bf == 0){subRL->_bf = 0;parent->_bf = 0;subR->_bf = 0;}else if (bf == 1){subRL->_bf = 0;parent->_bf = -1;subR->_bf = 0;}else if (bf == -1){subRL->_bf = 0;parent->_bf = 0;subR->_bf = 1;}else{// subLR->_bf旋转前就有问题assert(false);}}
❤️结语
一起加油

相关内容
热门资讯
喜欢穿一身黑的男生性格(喜欢穿...
今天百科达人给各位分享喜欢穿一身黑的男生性格的知识,其中也会对喜欢穿一身黑衣服的男人人好相处吗进行解...
网络用语zl是什么意思(zl是...
今天给各位分享网络用语zl是什么意思的知识,其中也会对zl是啥意思是什么网络用语进行解释,如果能碰巧...
发春是什么意思(思春和发春是什...
本篇文章极速百科给大家谈谈发春是什么意思,以及思春和发春是什么意思对应的知识点,希望对各位有所帮助,...
苏州离哪个飞机场近(苏州离哪个...
本篇文章极速百科小编给大家谈谈苏州离哪个飞机场近,以及苏州离哪个飞机场近点对应的知识点,希望对各位有...
为什么酷狗音乐自己唱的歌不能下...
本篇文章极速百科小编给大家谈谈为什么酷狗音乐自己唱的歌不能下载到本地?,以及为什么酷狗下载的歌曲不是...
家里可以做假山养金鱼吗(假山能...
今天百科达人给各位分享家里可以做假山养金鱼吗的知识,其中也会对假山能放鱼缸里吗进行解释,如果能碰巧解...
四分五裂是什么生肖什么动物(四...
本篇文章极速百科小编给大家谈谈四分五裂是什么生肖什么动物,以及四分五裂打一生肖是什么对应的知识点,希...
华为下载未安装的文件去哪找(华...
今天百科达人给各位分享华为下载未安装的文件去哪找的知识,其中也会对华为下载未安装的文件去哪找到进行解...
怎么往应用助手里添加应用(应用...
今天百科达人给各位分享怎么往应用助手里添加应用的知识,其中也会对应用助手怎么添加微信进行解释,如果能...
客厅放八骏马摆件可以吗(家里摆...
今天给各位分享客厅放八骏马摆件可以吗的知识,其中也会对家里摆八骏马摆件好吗进行解释,如果能碰巧解决你...