第四章 二次型

文章目录

• 第四章 二次型
• • 一、二次型定义
  • 二、合同变换
  • • 1.线性变换
    • 2.矩阵合同
    • • 标准型和规范型
    • 3.惯性定理
  • 三、正定二次型

一、二次型定义

如果系数a_ij全为实数，那么为实二次型。上述二次型展开式可表示用矩阵为

可以看出，二次型矩阵A是一个对称矩阵，也就是满足A^T=A，一个实对称矩阵对应的则是一个实二次型。一个二次型有多种写法，也有多个展开式，但是二次型矩阵是唯一的，各个等价的二次型展开式能够化为同一个二次型矩阵

二、合同变换

1.线性变换

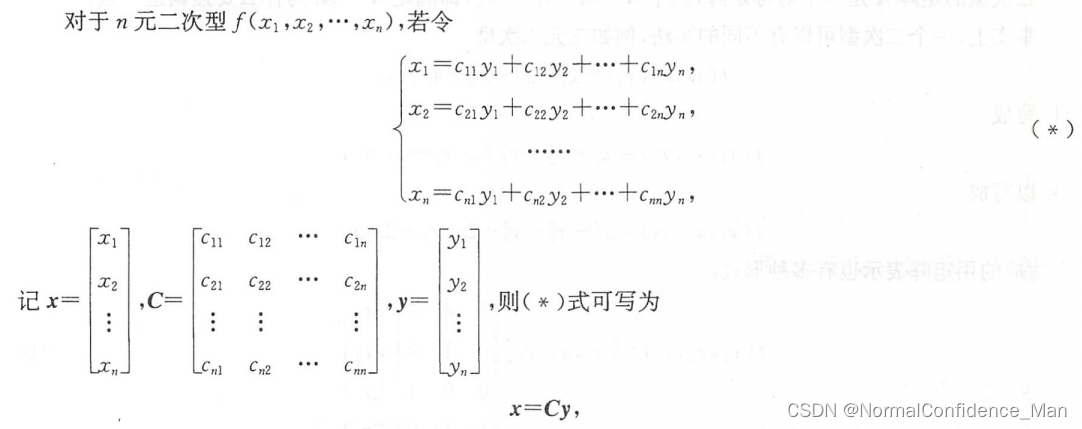
那么称*为线性变换，C为线性变换的系数矩阵，如果系数矩阵可逆，那么称为可逆线性变换（常用于配方法），如果是正交矩阵，则称为正交矩阵（用于正交变换法 ）。

给出二次型f(x)=xTAxf(x)=x^TAxf(x)=xTAx，令x=Cy，那么就有f(x)=(Cy)TA(CY)=yT(CTAC)yf(x)=(Cy)^TA(CY)=y^T(C^TAC)yf(x)=(Cy)TA(CY)=yT(CTAC)y记B=C^TAC，那么就有f(x)=yTBy=g(y)f(x)=y^TBy=g(y)f(x)=yTBy=g(y)，也就是说二次型f(x)通过线性变换x=Cy变成了新的二次型g(y)

2.矩阵合同

设n阶矩阵A、B是二次型f(x)和g(y)的二次型矩阵，如果存在可逆矩阵C使得CTAC=BC^TAC=BCTAC=B那么A和B合同，此时称f(x)和g(y)为合同二次型。

性质：

1. 反身性：A和自身合同
2. 对称性：A合同于B，则B合同于A
3. 传递性：A和B合同，B和C合同，则A和C合同
4. 如果A和B合同，则有r(A)=r(B)，因此可逆线性变换不会改变二次型的秩
5. 根据4.可推导出，和对称矩阵合同的也是对称矩阵。因为如果A、B为对称阵，则有BT=(CTAC)T=CTATC=CTAC=BB^T=(C^TAC)^T=C^TA^TC=C^TAC=BBT=(CTAC)T=CTATC=CTAC=B，

判断同阶实对称矩阵A、B是否合同：
1.用定义法：A，B合同⇔\Leftrightarrow⇔存在可逆矩阵C使得C^TAC=B
2.用正负惯性指数：A，B合同 ⇔\Leftrightarrow⇔A，B正负惯性指数相同
3.用传递性：A和B合同，B和C合同，则A和C合同
4.同阶实对称矩阵A,B相似必然合同
5.特征值相同、特征向量相同无法推出A、B合同

对于合同的判别，一定要结合矩阵相似联系理解，并且充分认识到矩阵合同和矩阵相似两个概念是如何联系起来的

题型：

• 已知A、ΛA、\LambdaA、Λ，求可逆矩阵C使得CTAC=ΛC^TAC=\LambdaCTAC=Λ
• 已知A，B，求可逆矩阵C使得CTAC=BC^TAC=BCTAC=B（需要重点关注）

在此需要将以下概念对比记忆：矩阵合同，矩阵正交，矩阵相似，矩阵等价，向量组等价

标准型和规范型

如果二次型中只含有平方项，没有交叉项，也就是形如d1x12+d2x22+d3x32+...dnxn2+d_1x_1^2+d_2x_2^2+d_3x_3^2+...d_nx_n^2+d1​x12​+d2​x22​+d3​x32​+...dn​xn2​+的称之为标准型。
若标准型中，系数d_i仅为0，-1,1这三种，则称该二次型为规范型

如果二次型f(x)=xTAxf(x)=x^TAxf(x)=xTAx合同于标准型，则称其为合同标准型。任何二次型都可以通过配方法化为标准型和规范型，也就是任何实对称矩阵A都存在可逆矩阵C，使得CTAC=ΛC^TAC=\LambdaCTAC=Λ。任何二次型可以通过正交变换化为标准型，也就是Q−1AQ=QTAQ=ΛQ^{-1}AQ=Q^TAQ=\LambdaQ−1AQ=QTAQ=Λ。需要注意的是，配方法中的C矩阵并非是特征向量矩阵，因为C不一定是正交矩阵，不存在C^-1=C^T

二次型化标准型的方法：
1.配方法
将某个变量的平方项和其相关的混合项合并在一起，配成一个完全平方项。如果不含平方项则通过x1=y1+y2,x2=y1−y2x_1=y_1+y_2, x_2=y_1-y_2x1​=y1​+y2​,x2​=y1​−y2​和平方差公式来创造平方项

2.正交变换法
正交变换法的思想如下：
先求出矩阵A的特征值和特征向量，并且组成矩阵：AQ=QΛ⇔Q−1AQ=ΛAQ=Q\Lambda \Leftrightarrow Q^{-1}AQ=\LambdaAQ=QΛ⇔Q−1AQ=Λ，接着通过施密特正交化，将矩阵Q改造成正交矩阵，则有Q^-1=Q^T，因此Q−1AQ=QTAQ=ΛQ^{-1}AQ=Q^TAQ=\LambdaQ−1AQ=QTAQ=Λ，符合标准型定义

通过正交变换我们可知：Q−1AQ=QTAQ=ΛQ^{-1}AQ=Q^TAQ=\LambdaQ−1AQ=QTAQ=Λ，也就是xTAx=yT(QTAQ)y=yTΛyx^TAx=y^T(Q^TAQ)y=y^T\Lambda yxTAx=yT(QTAQ)y=yTΛy，也就是x=Qy，那么xTx=(Qy)TQy=yTQTQyx^Tx=(Qy)^TQy=y^TQ^TQyxTx=(Qy)TQy=yTQTQy由于QT=Q−1Q^T=Q^{-1}QT=Q−1，所以xTx=yTyx^Tx=y^TyxTx=yTy

基本步骤

3.惯性定理

无论采用何种可逆线性变换将二次型化为标准型或者规范型，其中的正项个数p，负项个数q都是不变的，p称为正惯性指数，q称为负惯性指数

三、正定二次型

二次型正定的充要条件
n元二次型f=x^TAx正定⇔\Leftrightarrow⇔对x≠0x\neq0x​=0有x^TAx>0
⇔\Leftrightarrow⇔f的正惯性指数p=n
⇔\Leftrightarrow⇔存在可逆矩阵D使得A=D^TD
⇔\Leftrightarrow⇔A和E合同
⇔\Leftrightarrow⇔A的特征值全大于0
⇔\Leftrightarrow⇔A的全部顺序主子式大于0（最容易用作判断是否正定）

二次型正定的必要条件

1. a_ii>0
2. |A|>0

重要结论

• 如果A正定，则A^-1,A^*, A^m,kA,A^T,C^TAC都正定，而且A^T=A
• 如果A，B正定，那么A+B正定，其对角分块矩阵正定
• A,B正定，而AB正定的充要条件是AB=BA。（对比记忆：正交阵相乘必然正交）
• 如果矩阵A正定并且正交，那么A=E