回溯法求解n个元素的集合的幂集
创始人
2024-01-20 15:47:06
0次
目录
1.回溯法
2.集合的幂集本质问题
3.集合的幂集
(1)集合
(2)求解集合的幂集
(3)算法描述
(4)算法实现
(5)算法拓展
1.回溯法
- 回溯法也是设计递归过程的一种重要方法,求解过程实质上是先序遍历一棵“状态树”的过程。
- 回溯法的应用
- 九宫格问题
- 八皇后问题
- 数独问题
- 求集合的幂集问题
2.集合的幂集本质问题
提示:如果读者学习过《算法设计与分析》的话,那么应该很清楚,其中有一类问题是可以使用分治法进行求解的,那什么是分治法呢?
- 分治法:就是将原问题划分若干个性质相同的小问题,并对划分的子问题进行求解。
- 分治过程:
- 将一个问题划分为同一类型的若干子问题,子问题最好规模相同。
- 对这些子问题求解。
- 合并这些子问题的解,以得到原始问题的答案。
3.集合的幂集
(1)集合
提示:集合的幂集就是集合A的所有子集所组成的集合。
题目:要求求n个元素的集合的幂集!
假设这里有三个元素:A={1,2,3},那么集合A的幂集?
ρ(A)={{1,2,3},{1,2},{1,3},{1},{2,3},{2},{3},Φ}
如下图所示:
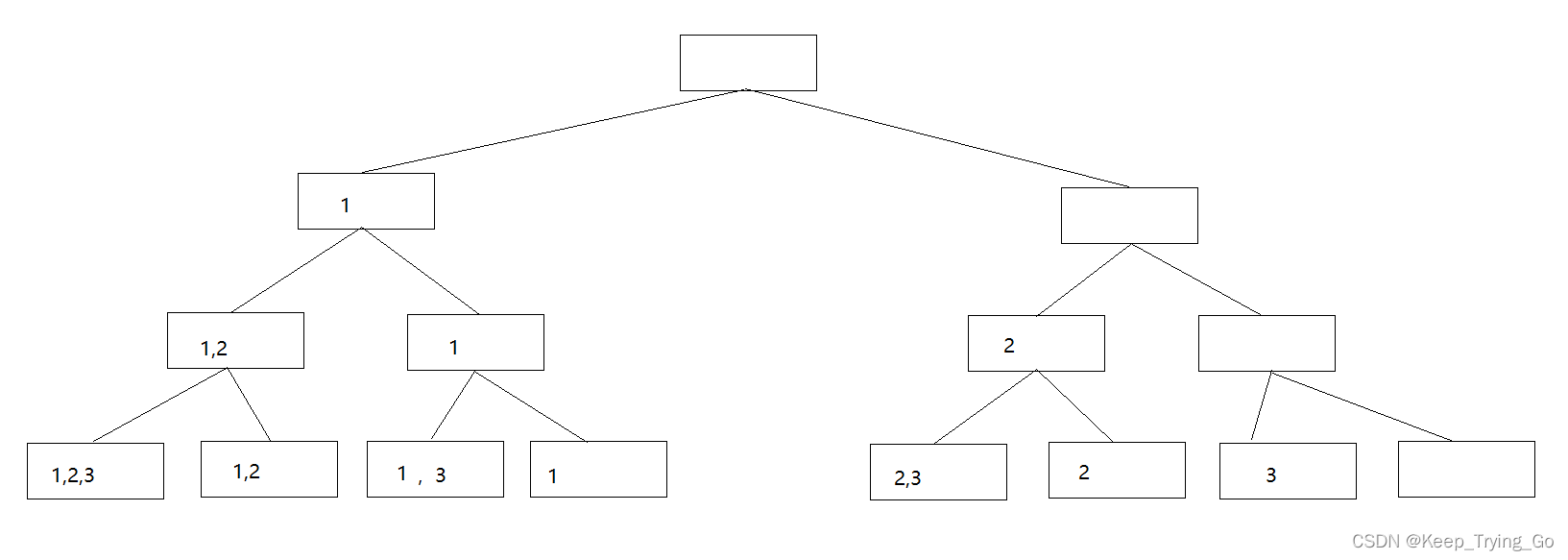
(2)求解集合的幂集
提示:求解ρ(A)集合的过程可以看成是依次对集合A中元素进行“取”或者“舍(弃)”的过程,通过上面也可以看到是一棵二叉树来表示幂集元素的状态变化状况。
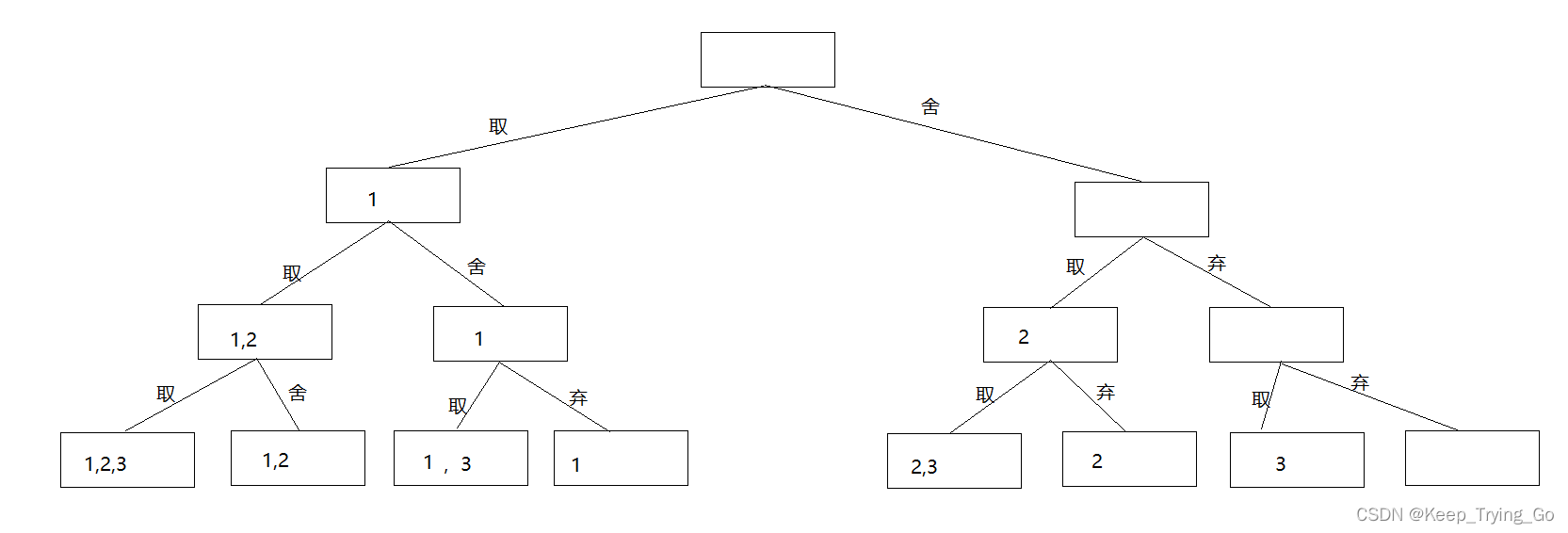
- 过程:
- 树中的根节点表示幂集元素的初始状态(为空集);
- 叶子节点表示它的终结状态中幂集ρ(A)的8个元素;
- 第i层(i=1,2,3,...,n)层的分支节点,则表示已对集合A中前i-1个元素进行了取/舍处理的当前状态(其中左分支表示“取”,右分支表示“舍”);
- 将上述问题求解集合的幂集转换为先序遍历这棵状态树的过程。
(3)算法描述
void Powerset(int i,int n){//初始调用:Powerset(1,n)if(i>n){输出幂集的其中一个元素 }else{取第i个元素Powerset(i+1,n);舍第i个元素 Powerset(i+1,n);}
} 提示:上述的关键问题是怎么表示“取”和“舍”的过程。
疑问:为什么说求幂集元素的过程是先序遍历状态树的过程呢?
解释:首先要清楚先序遍历的过程是先根后左再右,这样的一个遍历过程;那么在该代码中怎么体现这个先序遍历的过程的呢?从上面画出的集合的幂集二叉树图,可以看到,其实就是通过“取”或者“舍”这个方法来实现的,代码中的auxset[i-1]=set[i-1]就是在进入“左子树”的过程,也就是“取”的过程;而auxset[i-1]=0,则是在进入“右子树”的过程,也就是在“舍”的过程。如果读者还是感觉有点抽象,可以在纸上模拟一下这个过程就能深有体会了。
(4)算法实现
#include
#include
#include#define maxn 10//使用数组set表示集合
int set[maxn];
//使用辅助数组auxset表示取和舍的过程
int auxset[maxn];void init(int n){for(int i=0;in){for(int j=0;j 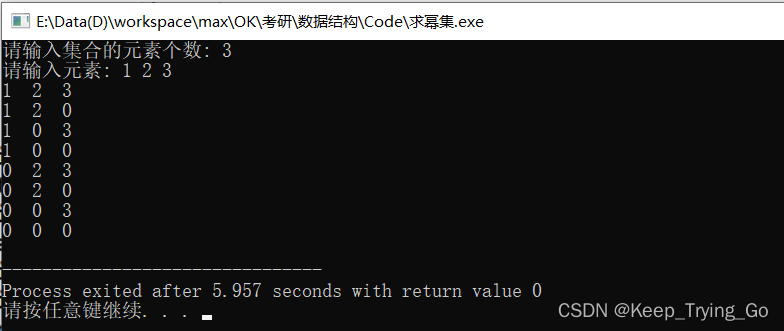
提示:我这里输出0的原因主要是因为更能表达空集。
(5)算法拓展
- 假设以线性表表示集合,则求解后的算法如下所示
实现一个顺序存储的线性表
使用C语言实现单链表的功能(带头节点)
使用C语言实现动态顺序表
使用C语言实现静态顺序表
void GetPowerset(int i,List A,List B){//线性表A表示集合,线性表B表示幂集ρ(A)的一个元素//局部变量K为进入函数时B的当前长度,第一次调用本函数时,B为空表,i=1if(i>ListLength(A)){Output(B);}else{GetElem(A,i,x);int k=ListLength(B);ListInsert(B,k+1,x);GetPowerset(i+1,A,B);ListDelete(B,k+1,x);GetPowerset(i+1,A,B);}
}参考书籍《数据结构》严蔚敏
相关内容
热门资讯
喜欢穿一身黑的男生性格(喜欢穿...
今天百科达人给各位分享喜欢穿一身黑的男生性格的知识,其中也会对喜欢穿一身黑衣服的男人人好相处吗进行解...
网络用语zl是什么意思(zl是...
今天给各位分享网络用语zl是什么意思的知识,其中也会对zl是啥意思是什么网络用语进行解释,如果能碰巧...
发春是什么意思(思春和发春是什...
本篇文章极速百科给大家谈谈发春是什么意思,以及思春和发春是什么意思对应的知识点,希望对各位有所帮助,...
苏州离哪个飞机场近(苏州离哪个...
本篇文章极速百科小编给大家谈谈苏州离哪个飞机场近,以及苏州离哪个飞机场近点对应的知识点,希望对各位有...
为什么酷狗音乐自己唱的歌不能下...
本篇文章极速百科小编给大家谈谈为什么酷狗音乐自己唱的歌不能下载到本地?,以及为什么酷狗下载的歌曲不是...
家里可以做假山养金鱼吗(假山能...
今天百科达人给各位分享家里可以做假山养金鱼吗的知识,其中也会对假山能放鱼缸里吗进行解释,如果能碰巧解...
四分五裂是什么生肖什么动物(四...
本篇文章极速百科小编给大家谈谈四分五裂是什么生肖什么动物,以及四分五裂打一生肖是什么对应的知识点,希...
华为下载未安装的文件去哪找(华...
今天百科达人给各位分享华为下载未安装的文件去哪找的知识,其中也会对华为下载未安装的文件去哪找到进行解...
怎么往应用助手里添加应用(应用...
今天百科达人给各位分享怎么往应用助手里添加应用的知识,其中也会对应用助手怎么添加微信进行解释,如果能...
客厅放八骏马摆件可以吗(家里摆...
今天给各位分享客厅放八骏马摆件可以吗的知识,其中也会对家里摆八骏马摆件好吗进行解释,如果能碰巧解决你...