红黑树

二分查找

二叉树

二叉平衡树

平衡因子不超1

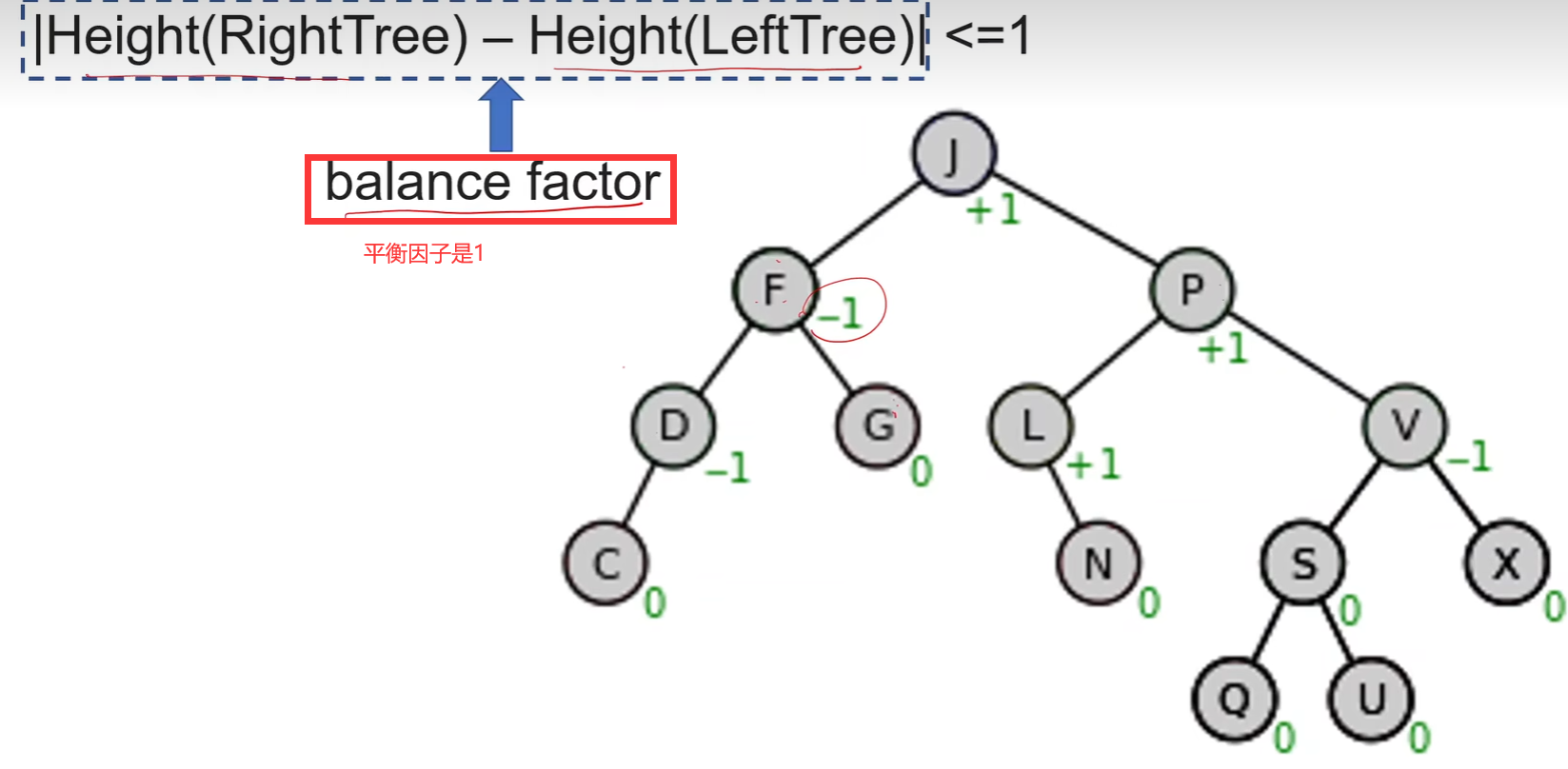
查找和二叉查找一样的 删除和插入比较复杂

四种失去平衡的方法

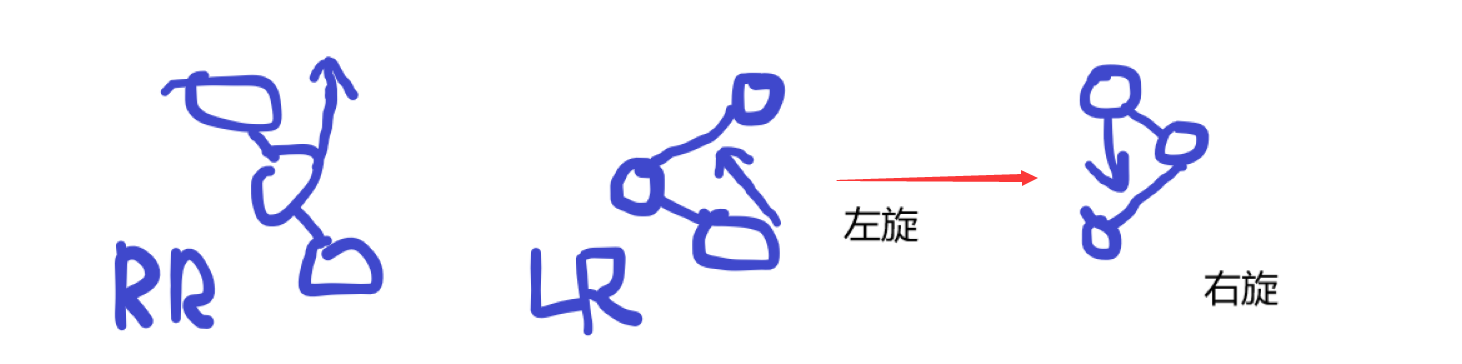
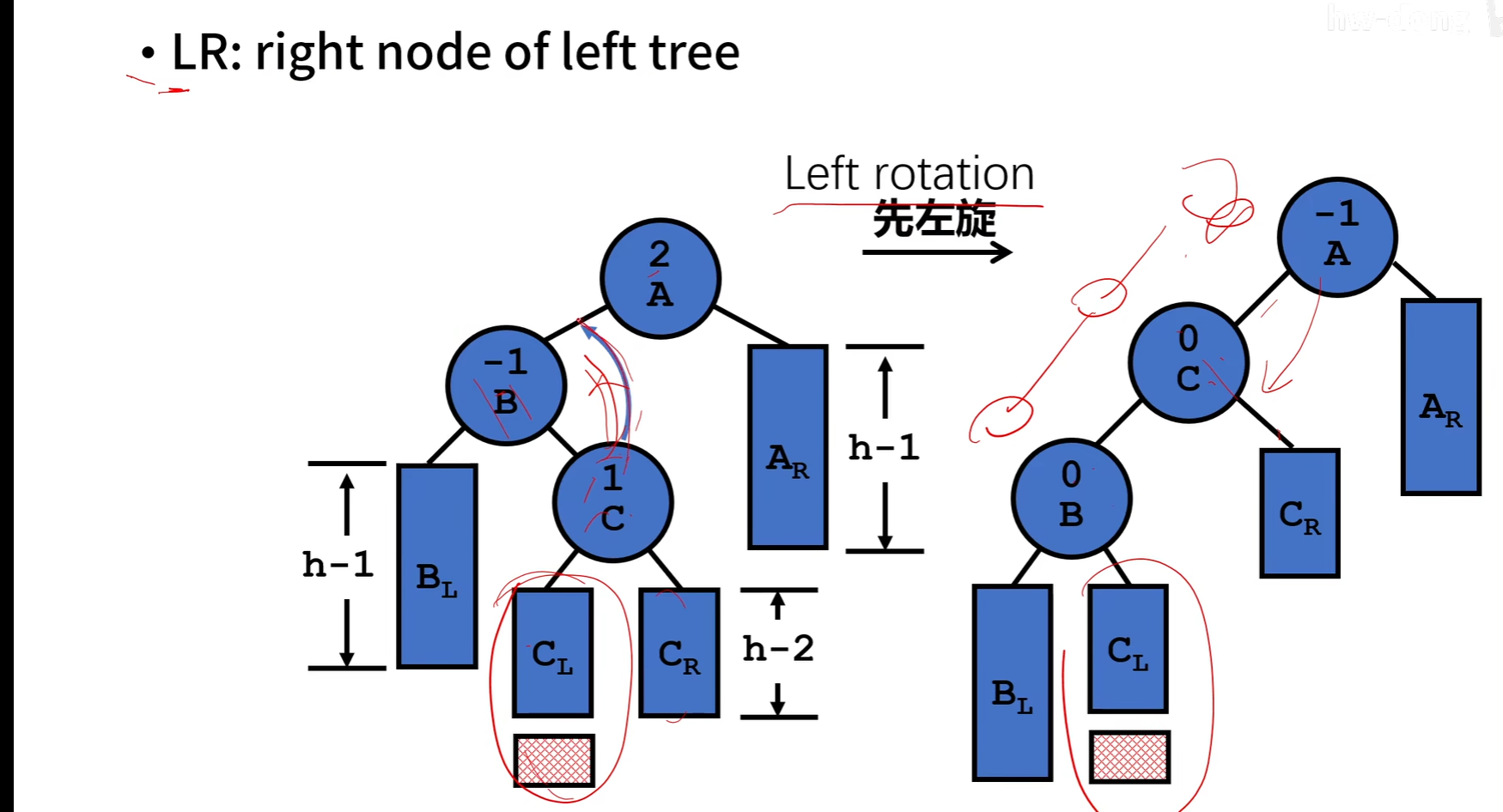
LR 两步

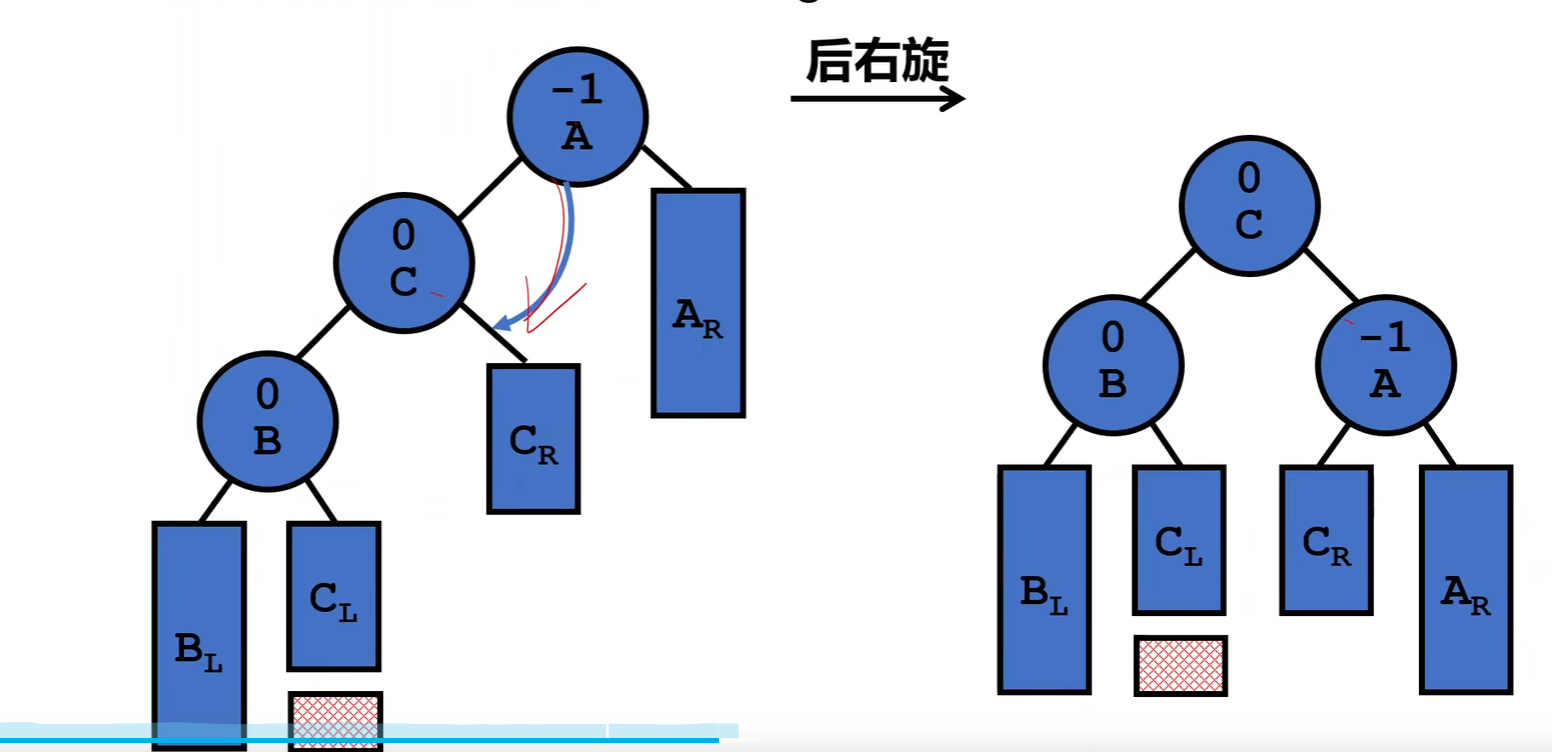
RL 两步

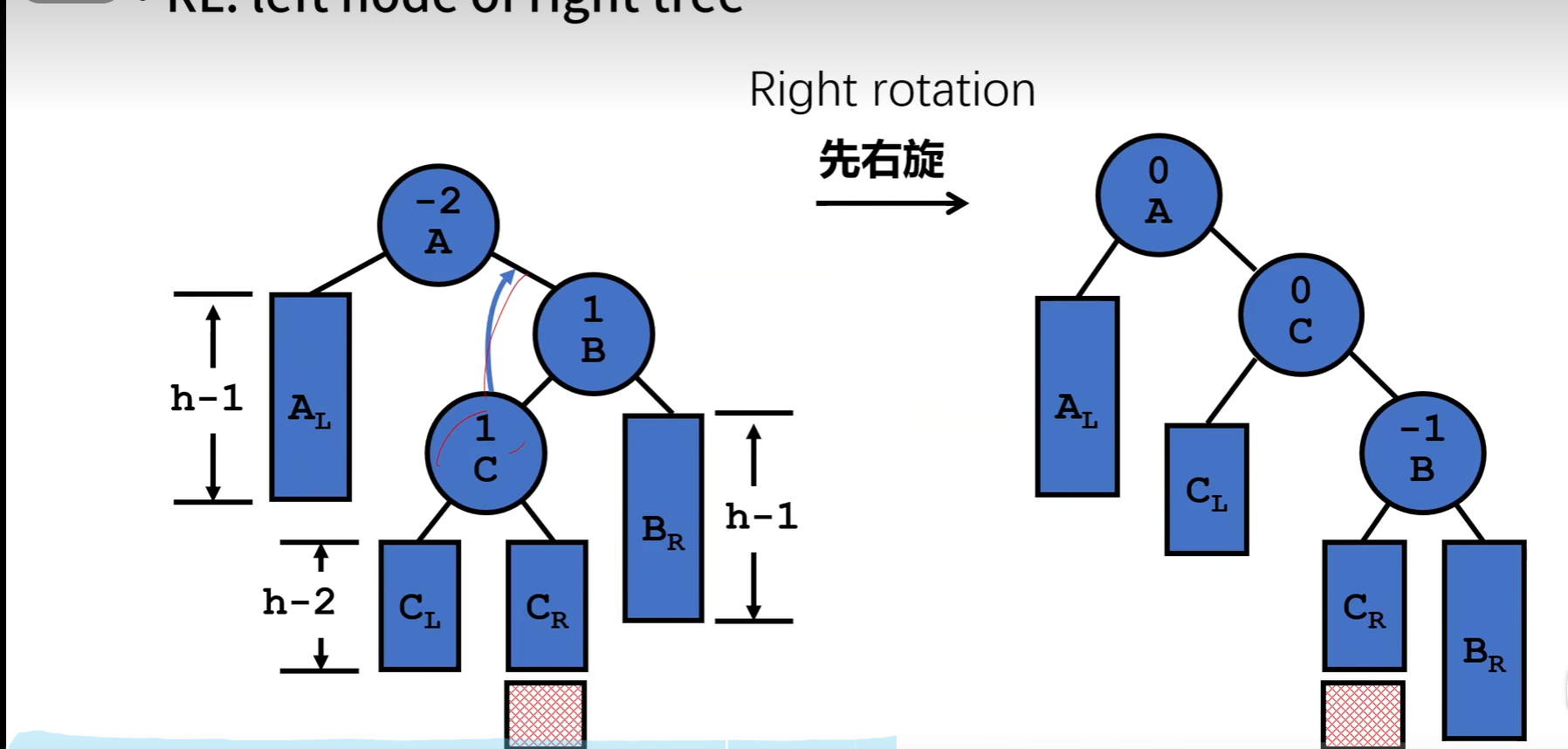
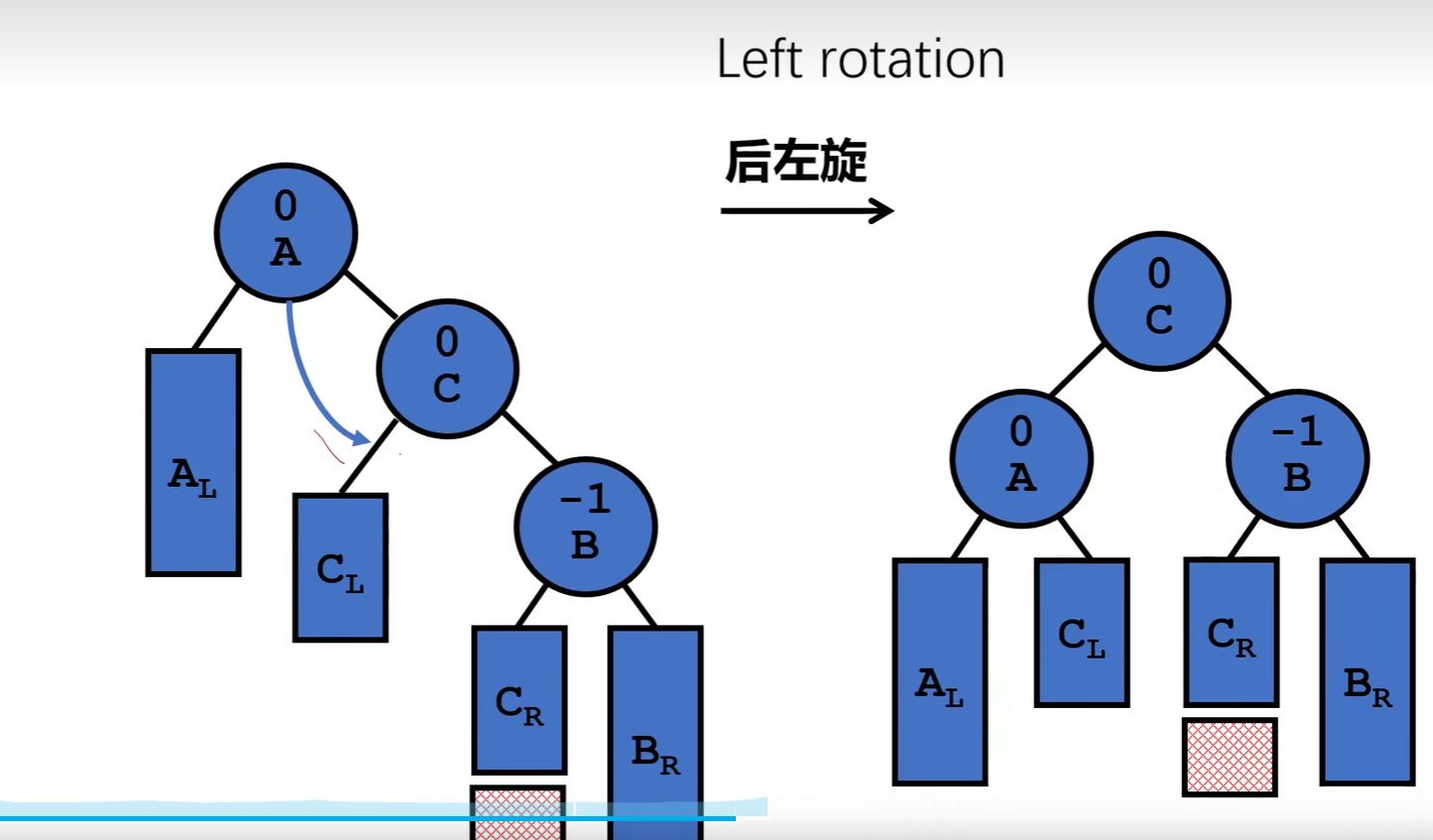
不断旋转比较耗时 进一步改进：

红黑树RBT

调整的次数少 平衡性不如二叉平衡树 ，

插入删除频繁的使用红黑树，不频繁的使用二叉平衡树。

（这里的空节点是叶子节点，与以往太不一样）

1.结点是红色或黑色。

2.根结点是黑色。

3.每个叶子结点都是黑色的空结点（NIL结点）。

4.红属性 ：每个红色结点的两个子结点都是黑色。

5.黑属性：每一个结点到其每个叶子的所有路径都包含相同数目的黑色结点。

The height of the red-black tree is at most：
2 log2(n+ 1)

新插入的是红色

• 父红，父兄弟红 那么 父亲和父亲兄弟 变黑，爷爷变红（这个是一直向上重复的，如果爷爷是根结点不用变 ）

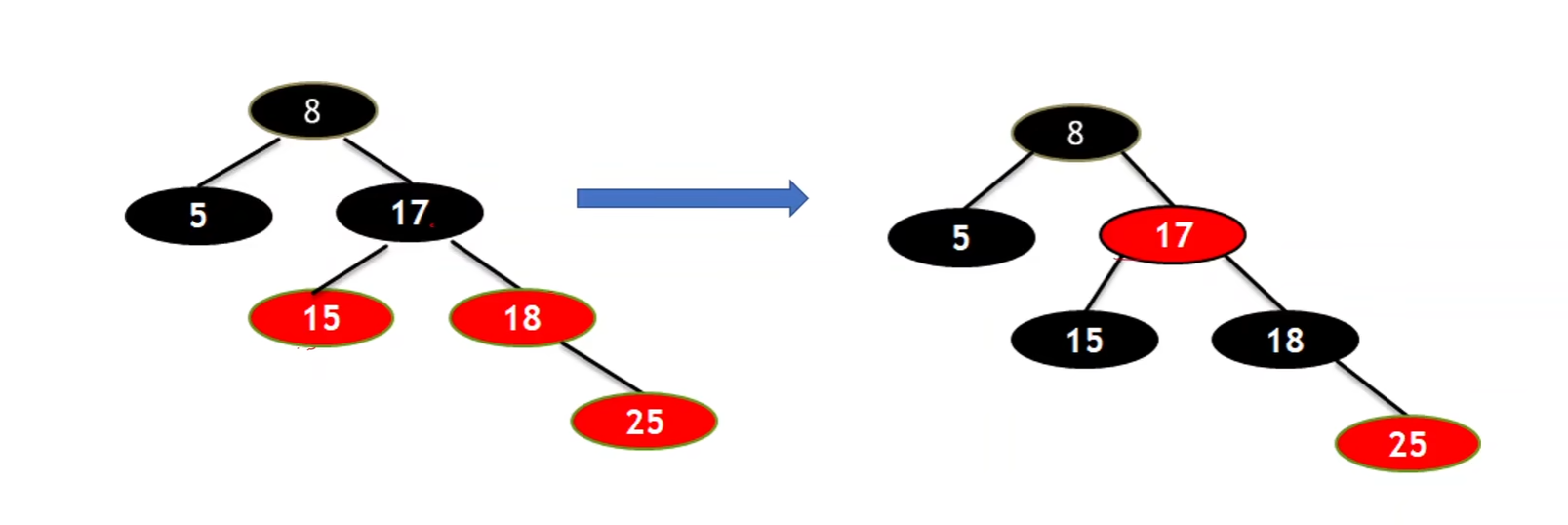
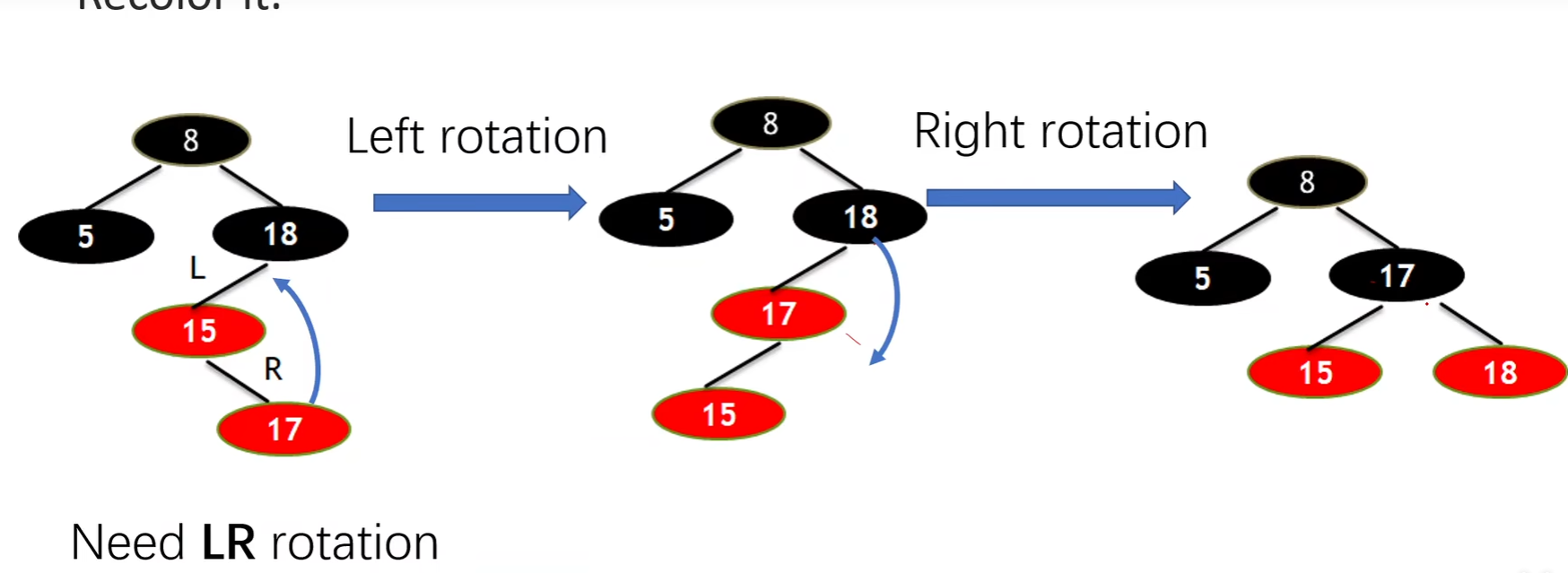
• 父红，父无兄弟或者父兄弟是黑 那么 先旋转（ll或者rr或者lr或者rl应该是） 后重新上色

给定下面这颗红黑树，新插入的结点是21：

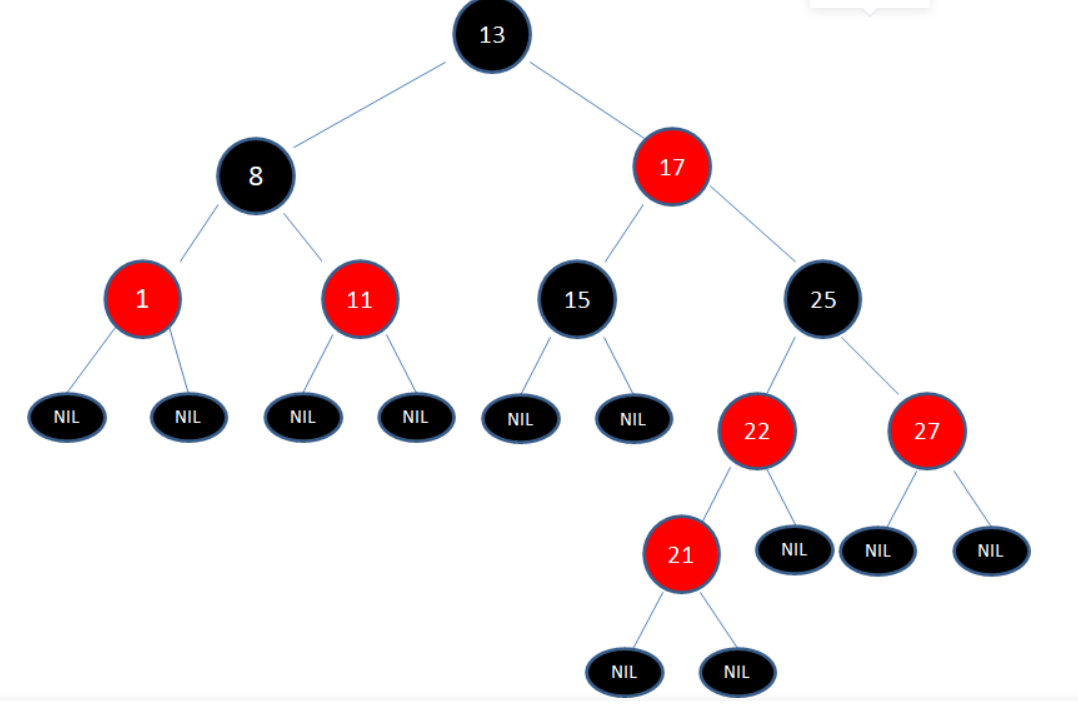
显然，新结点21和它的父结点22是连续的红色结点，违背了规则4，我们应该如何调整呢？

新结点的父结点和叔叔结点都是红色。

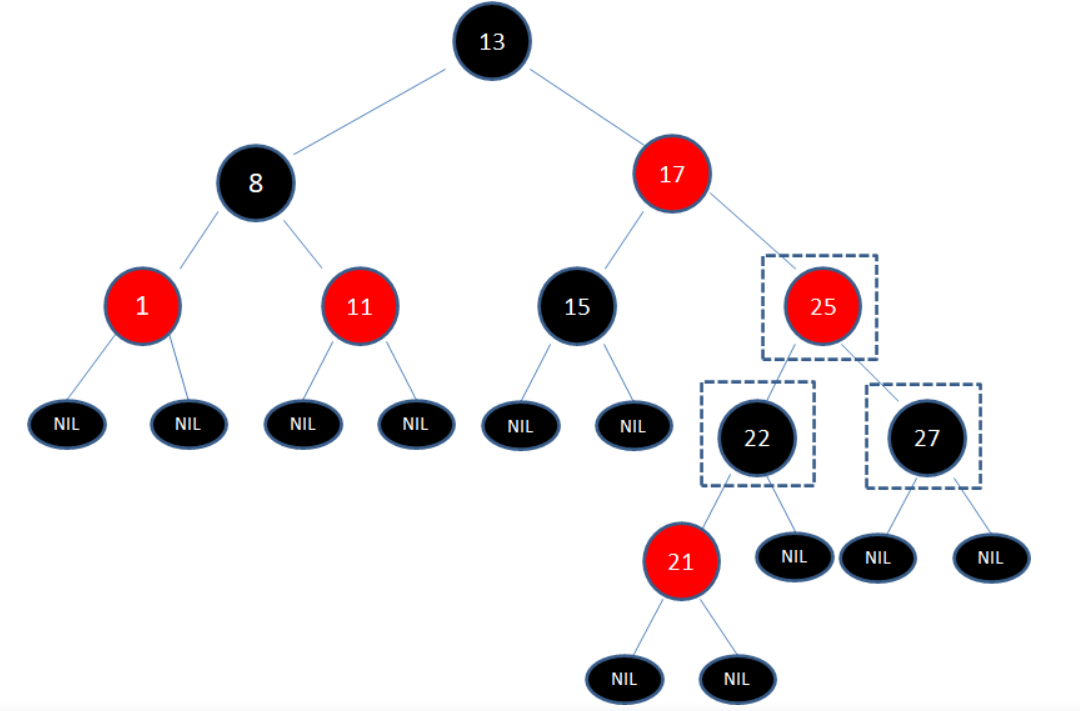
于是我们经过三次变色，22变为黑色，25变为红色，27变为黑色：

经过上面的调整，以结点25为根的子树符合了红黑树规则，但结点25和结点17成为了连续的红色结点

于是，我们把结点25看做一个新结点，正好符合：

“新结点的父结点是红色，叔叔结点是黑色或者没有叔叔，且新结点是父结点的右孩子，父结点是祖父结点的右孩子”

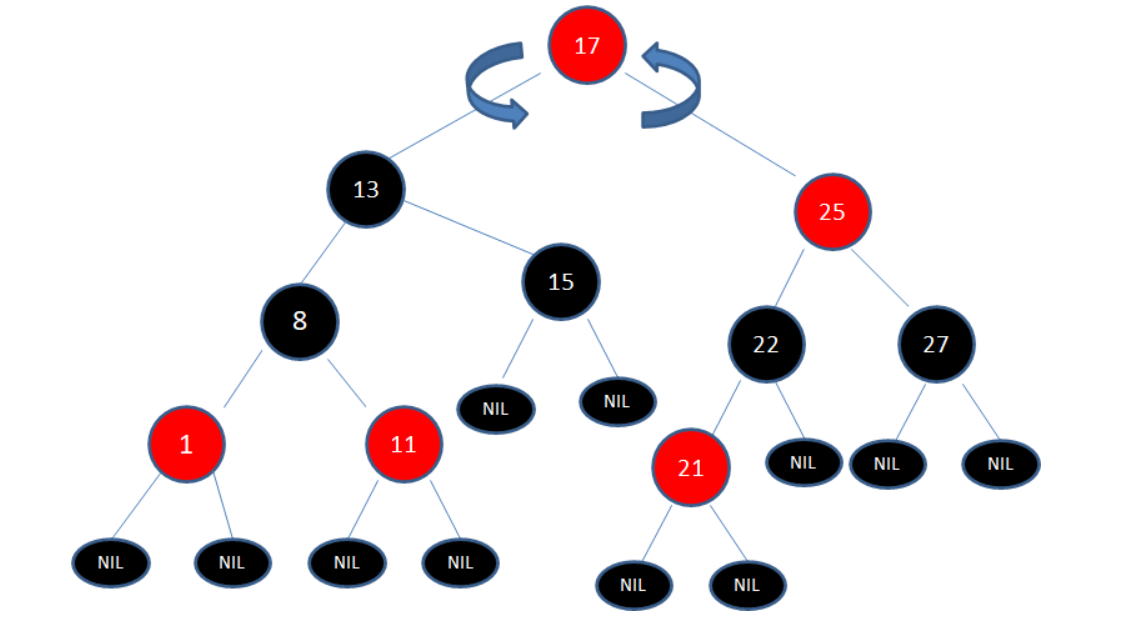
于是我们以根结点13为轴进行左旋转，使得结点17成为了新的根结点：

接下来，让结点17变为黑色，结点13变为红色：

如此一来，我们的红黑树变得重新符合规则。

删除比插入更复杂

数据库为什么不用红黑树而用B+树？

AVL树和红黑树基本都是存储在内存中才会使用的数据结构。而数据库中的数据的索引会非常大，所以为了减少内存的占用，索引会被存储到磁盘文件中，此时影响数据库查询效率的主要因素就是磁盘的IO次数。AVL树和红黑树由于一个父节点只能存储两个子节点。所以使用AVL树或红黑树存储大规模数据时，树的深度就会很深，此时磁盘的IO次数也会大幅度增加。B+树中一个父节点有多个子节点，减少了树的深度，磁盘IO次数也相应的减少。

索引的数据结构会被存储在磁盘中，每次查询都需要到磁盘中访问，对于红黑树，树的高度可能会非常的高，会进行很多次的磁盘IO，效率会非常低，B+树的高度一般为2-4，也就是说在最坏的条件下，也最多进行2到4次磁盘IO，这在实际中性能时非常不错的

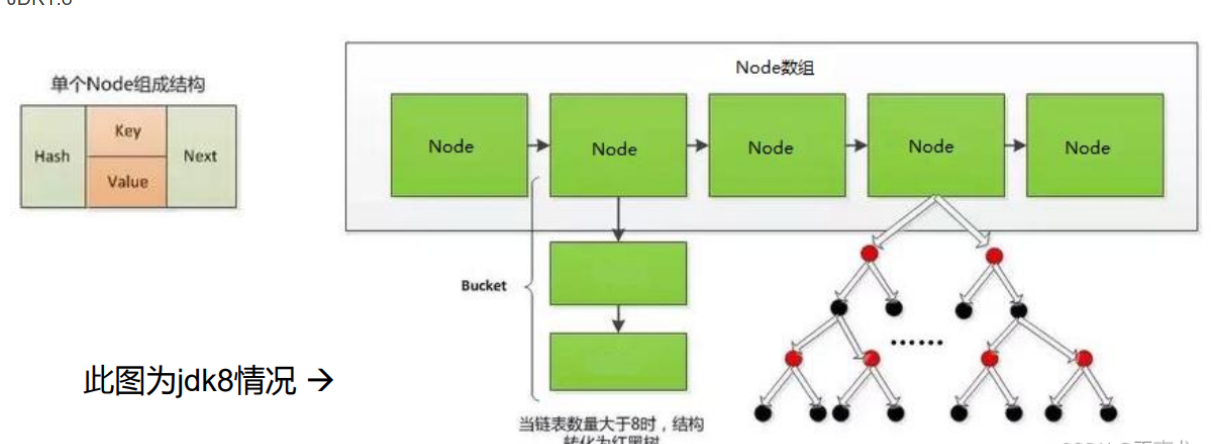
java中的BRT

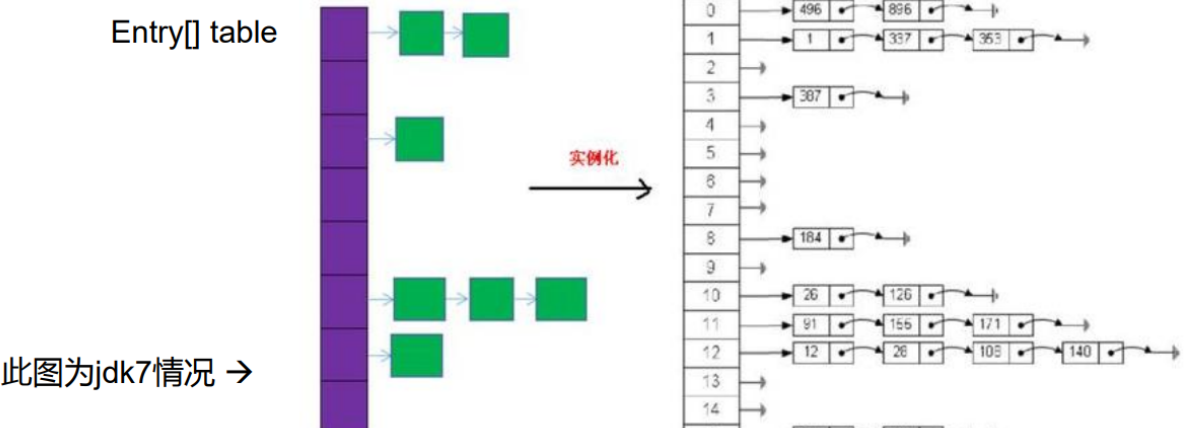
JDK 7及以前版本：HashMap是数组+链表结构(即为链地址法)
JDK 8版本发布以后：HashMap是数组+链表+红黑树实现。