算法60天：day46

• 动态规划-单词拆分
• 动态规划-多重背包问题
• 动态规划-背包总结

动态规划-单词拆分

力扣链接

class Solution {
public:bool wordBreak(string s, vector& wordDict) {unordered_set wordSet(wordDict.begin(),wordDict.end());vector dp(s.size() + 1 , false);dp[0] = true;for(int i = 1; i <= s.size(); i++){for(int j = 0; j < i; j++){string word = s.substr(j , i - j);if(wordSet.find(word) != wordSet.end() && dp[j]){dp[i] = true;}}}return dp[s.size()];}
};

动态规划-多重背包问题

其实就是将01背包中限制条件：每个只能取一次展开来

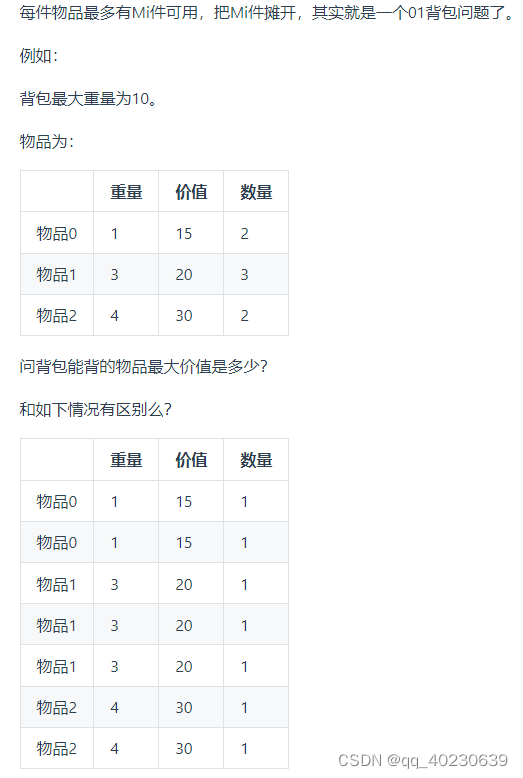
void test_multi_pack() {vector weight = {1, 3, 4};vector value = {15, 20, 30};vector nums = {2, 3, 2};int bagWeight = 10;for (int i = 0; i < nums.size(); i++) {while (nums[i] > 1) { // nums[i]保留到1，把其他物品都展开weight.push_back(weight[i]);value.push_back(value[i]);nums[i]--;}}vector dp(bagWeight + 1, 0);for(int i = 0; i < weight.size(); i++) { // 遍历物品for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);}for (int j = 0; j <= bagWeight; j++) {cout << dp[j] << " ";}cout << endl;}cout << dp[bagWeight] << endl;}
int main() {test_multi_pack();
}

动态规划-背包总结

一：01背包
1、一维dp数组01背包只能先遍历物品再遍历背包容量，且第二层for循环是从大到小遍历。

二、完全背包
1、纯完全背包的一维dp数组实现，先遍历物品还是先遍历背包都是可以的，且第二层for循环是从小到大遍历。
2、如果求组合数就是外层for循环遍历物品，内层for遍历背包。
3、如果求排列数就是外层for遍历背包，内层for循环遍历物品。

三、关于公式问题
1、如果是求最大价值则： dp[j] = max(dp[j], dp[j - nums[i]] + nums[i])
2、如果是求装满背包：dp[j] += dp[j - nums[i]]
3、如果是求最少num满足amount： dp[i] = min(dp[i - coins[j]] + 1, dp[i])