VINS学习（二）IMU预积分原理与实现

• 一、连续时间下的IMU积分
• 二、连续时间下的IMU预积分
• 三、离散时间下的IMU预积分
• • 1. 欧拉法
  • 2. 中值法
• 四、连续时间下的IMU状态误差传递
• 五、离散时间下的IMU状态误差传递
• 六、预积分量关于零偏的雅克比
• 七、VINS代码实践
• • 1.预积分类的数据成员与构造函数
  • 2.添加IMU数据
  • 3.根据IMU数据进行预积分

一、连续时间下的IMU积分

IMU测量值是在IMU坐标系中测量的，它受到加速度偏置ata_tat​、陀螺仪偏置btb_tbt​和噪声nan_ana​的影响。假设加速度计和陀螺仪测量值中的噪声为高斯噪声:

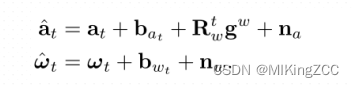
IMU坐标系对应bk,bk+1b_k, b_{k+1}bk​,bk+1​，对于图像帧kkk和k+1k+1k+1，在[𝑡𝑘,𝑡𝑘+1][𝑡_𝑘,𝑡_{𝑘+1}][tk​,tk+1​]时间间隔内对所有IMU测量值进行积分，可得第 k+1k+1k+1 帧的位置、速度和旋转 （PVQPVQPVQ）在世界坐标系下进行传递:

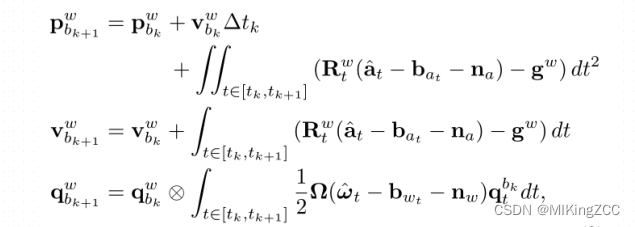
其中：

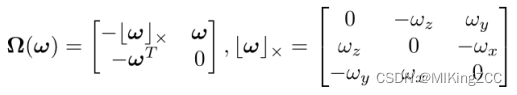
关于四元数q=[qw,qx,qy,qz]q=[q_w,q_x,q_y,q_z]q=[qw​,qx​,qy​,qz​]求导的补充：
q˙tw=lim⁡Δt→0qt+Δtw−qtwΔt=lim⁡Δt→0qtw⊗qt+Δtt−qtw⊗I(q)Δt=lim⁡Δt→0qtw⊗[cosθ2n⃗sinθ2]−qtw⊗[10⃗]Δt≈lim⁡Δt→0qtw⊗[1n⃗θ2]−qtw⊗[10⃗]Δt=lim⁡Δt→0[qt+Δtt]Rqtw−[I(q)]Rqtw=lim⁡Δt→0Ω(n⃗θ2)qtwΔt=12Ω(w^)qtw\begin{aligned} \dot{q}^w_t&= \lim_{\Delta t \to 0} \frac{q^w_{t+\Delta t} - q^w_t}{\Delta t} \\ &=\lim_{\Delta t \to 0} \frac{q^w_t \otimes q^{t}_{t+\Delta t}-q^w_t \otimes I_{(q)}}{\Delta t} \\ &=\lim_{\Delta t \to 0} \frac{q^w_t \otimes \begin{bmatrix} cos\frac{\theta}{2}\\ \vec{n}\frac{sin\theta}{2} \end{bmatrix}-q^w_t \otimes \begin{bmatrix} 1\\ \vec{0} \end{bmatrix}}{\Delta t} \\ &\approx\lim_{\Delta t \to 0} \frac{q^w_t \otimes \begin{bmatrix} 1\\ \frac{\vec{n}\theta}{2} \end{bmatrix}-q^w_t \otimes \begin{bmatrix} 1\\ \vec{0} \end{bmatrix}}{\Delta t} \\ &=\lim_{\Delta t \to 0} \frac{\begin{bmatrix} q^{t}_{t+\Delta t} \end{bmatrix}_R q^w_t - \begin{bmatrix} I_{(q)} \end{bmatrix}_R q^w_t}{} \\ &=\lim_{\Delta t \to 0} \frac{\Omega(\frac{\vec{n}\theta}{2} )q^w_t}{\Delta t} \\ &=\frac{1}{2}\Omega(\hat{w})q^w_t \end{aligned}q˙​tw​​=Δt→0lim​Δtqt+Δtw​−qtw​​=Δt→0lim​Δtqtw​⊗qt+Δtt​−qtw​⊗I(q)​​=Δt→0lim​Δtqtw​⊗[cos2θ​n2sinθ​​]−qtw​⊗[10​]​≈Δt→0lim​Δtqtw​⊗[12nθ​​]−qtw​⊗[10​]​=Δt→0lim​[qt+Δtt​​]R​qtw​−[I(q)​​]R​qtw​​=Δt→0lim​ΔtΩ(2nθ​)qtw​​=21​Ω(w^)qtw​​
关于四元数乘法的补充：

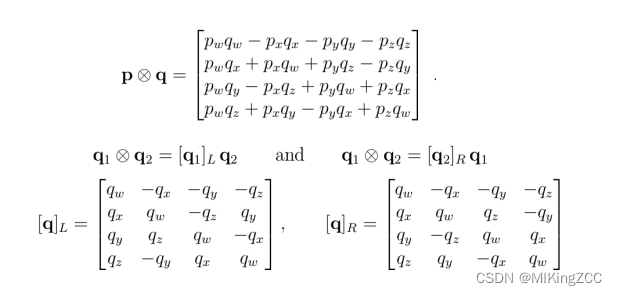
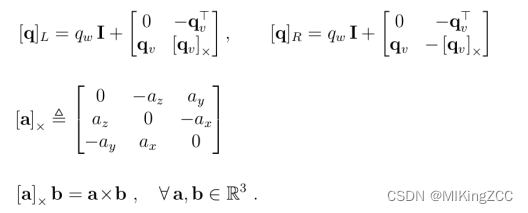
二、连续时间下的IMU预积分

在卡尔曼滤波中，假设了一阶马尔可夫性，当前时刻状态值只与上一时刻的状态值有关，所以历史时刻的状态不会发生改变，使用普通的方法对IMU进行积分，单向传播即可。但是，在当我们后端进行非线性优化时，历史时刻的状态变量PVQ以及IMU的bais会随着每次迭代而改变，由于IMU积分与上一时刻的状态量相关，所以每次调整完之后，都需要重新计算IMU积分， 造成重复转播，为了解决这个问题引入了IMU预积分方法：
将参考坐标系从世界坐标系（www）转变为当前帧坐标系（bkb_kbk​系):

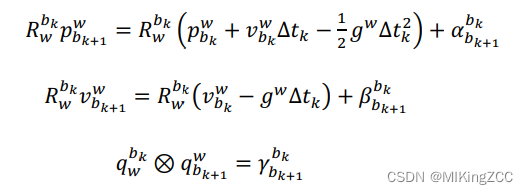
其中：

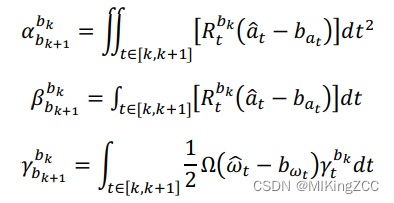
这样我们就得到了连续时刻的 IMU 预积分公式，可以发现，上式得到的 IMU 预积分的值只与不同时刻的a^t\hat a_ta^t​和w^t\hat w_tw^t​相关(实际上预积分值与我们优化变量IMU的bias 也是相关的，但是我们放在后面讨论，连续情况下的预积分先到此为止)。显然，当上一时刻的状态量变化时，预积分值不发生改变，只需要重新简单的计算加减法即可。

三、离散时间下的IMU预积分

1. 欧拉法

下面给出离散时刻的 IMU 预积分公式，首先按照论文中采用的欧拉法，给出第 iii 个 IMU时刻与第 i+1i+1i+1 个 IMU 时刻的变量关系为：

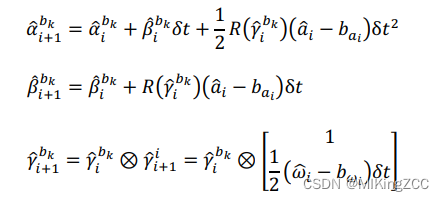
2. 中值法

下面给出代码中采用的基于中值法的 IMU 预积分公式，这里积分出来的是前后两帧之间的 IMU 增量信息，而不是当前帧时刻的物理量信息:
α^i+1bk=α^ibk+β^ibkδt+12α^ˉiδt2β^i+1bk=β^ibk+α^ˉiδtγ^i+1bk=γ^ibk⊗γ^i+1i=γ^ibk⊗[112ω^iδtˉ]\begin{aligned} \hat{\alpha}^{b_k}_{i+1} &=\hat{\alpha}^{b_k}_{i}+\hat{\beta}^{b_k}_{i}\delta t+\frac{1}{2}\bar{\hat{\alpha}}_i\delta t^2 \\ \hat{\beta}^{b_k}_{i+1} &=\hat{\beta}^{b_k}_{i}+\bar{\hat{\alpha}}_i \delta t \\ \hat{\gamma}^{b_k}_{i+1}&=\hat{\gamma}^{b_k}_{i} \otimes \hat{\gamma}^{i}_{i+1} = \hat{\gamma}^{b_k}_{i} \otimes \begin{bmatrix} 1 \\ \frac{1}{2} \bar{\hat{\omega}_i\delta t} \end{bmatrix} \end{aligned} α^i+1bk​​β^​i+1bk​​γ^​i+1bk​​​=α^ibk​​+β^​ibk​​δt+21​α^ˉi​δt2=β^​ibk​​+α^ˉi​δt=γ^​ibk​​⊗γ^​i+1i​=γ^​ibk​​⊗[121​ω^i​δtˉ​​]​
其中：
α^iˉ=12[qibk(α^i−bai)+qi+1bk(α^i+1bk−bαi)]ω^iˉ=12(ω^i+ω^i+1)−bωi\begin{aligned} \bar{\hat{\alpha}_i} &= \frac{1}{2}[q^{b_k}_i(\hat{\alpha}_i-b_{a_i})+q^{b_k}_{i+1}(\hat{\alpha}^{b_k}_{i+1}-b_{\alpha_i})] \\ \bar{\hat{\omega}_i }&= \frac{1}{2}(\hat{\omega}_i+\hat{\omega}_{i+1})-b_{\omega_i} \end{aligned}α^i​ˉ​ω^i​ˉ​​=21​[qibk​​(α^i​−bai​​)+qi+1bk​​(α^i+1bk​​−bαi​​)]=21​(ω^i​+ω^i+1​)−bωi​​​

四、连续时间下的IMU状态误差传递

IMU 在每一个时刻积分出来的值是有误差的，下面我们对误差进行分析。首先我们直接给出在 t 时刻误差项的导数为（更具体的推导可以参考我之前的一篇博客IMU预积分模型分析）：

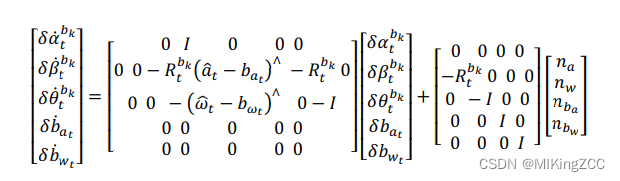
可以简写为：

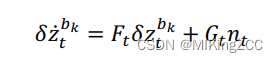
根据导数定义可知，下一时刻的均值预测为：

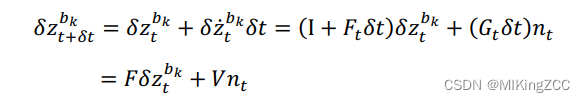
协方差预测公式如下：

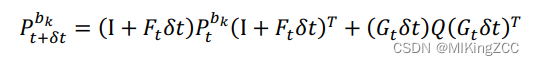
在协方差的迭代公式中初始值Pbkbk=0P^{b_k}_{b_k}=0Pbk​bk​​=0，QQQ表示噪声的协方差矩阵：

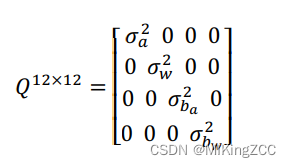
误差项的 Jacobian 初始值为Jbk=IJ_{b_k}=IJbk​​=I，迭代公式如下：

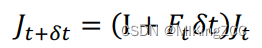
五、离散时间下的IMU状态误差传递

考虑离散时间下的IMU状态误差传递：
δzk+1=δzk+J(x)Δt\begin{aligned} \delta z_{k+1} &=\delta z_k +J(x) \Delta t\\ \end{aligned}δzk+1​​=δzk​+J(x)Δt​
利用连续时间下的推导，最终可以得到增量误差在离散形式下的矩阵形式：

最终离散时间下矩阵形式可以表达为：

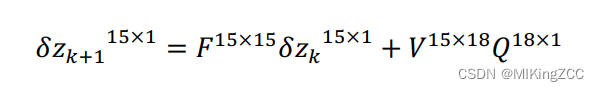
QQQ 为表示噪声项的对角协方差矩阵:

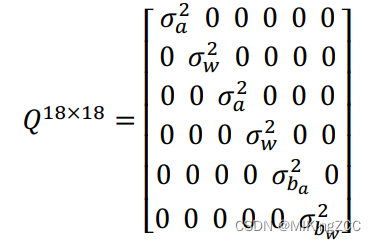
离散时间下预积分协方差矩阵的传递可以表示为（PkP_kPk​初值为0）：

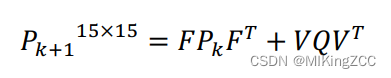
六、预积分量关于零偏的雅克比

在第二节中提到预积分值与我们优化变量IMU的bias 也是相关的，而bias 也是我们需要优化的变量，如果每次优化后因为bias改变需要重新计算预积分的话，那么预积分的引入将毫无意义。所以我们这里假设预积分的变化量与bias 是线性关系，则可以表示为：

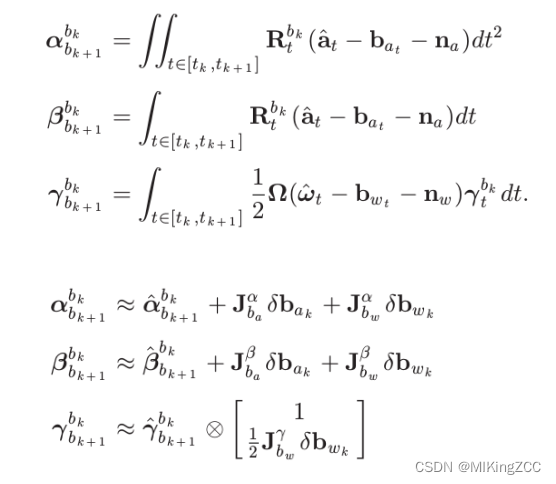
当优化后bais发生改变时，我们使用上式近似校正预积分结果，而不重新计算预积分。
显然这样计算会带来一个新的问题：Jbaα、Jbwα、Jbaβ、Jbwβ、JbwγJ^{\alpha}_{b_{a}}、J^{\alpha}_{b_w}、J^{\beta}_{b_a}、J^{\beta}_{b_w}、J^{\gamma}_{b_w}Jba​α​、Jbw​α​、Jba​β​、Jbw​β​、Jbw​γ​怎么计算。想要计算出这几个雅可比矩阵的闭式解是困难的，我们考虑估计值对本身的求导：Jzk+1=∂zk+1∂zkJ_{z_{k+1}}=\frac{\partial z_{k+1}}{\partial z_{k}}Jzk+1​​=∂zk​∂zk+1​​，显然有：
Jbaα=Jzk+1(0,1)Jbwα=Jzk+1(0,4)Jbaβ=Jzk+1(1,0)Jbwβ=Jzk+1(1,4)Jbwγ=Jzk+1(2,4)\begin{aligned} J^{\alpha}_{b_{a}} &= J_{z_{k+1}}(0,1)\\ J^{\alpha}_{b_w} &= J_{z_{k+1}}(0,4)\\ J^{\beta}_{b_a} &= J_{z_{k+1}}(1,0)\\ J^{\beta}_{b_w} &= J_{z_{k+1}}(1,4)\\ J^{\gamma}_{b_w} &= J_{z_{k+1}}(2,4) \end{aligned}Jba​α​Jbw​α​Jba​β​Jbw​β​Jbw​γ​​=Jzk+1​​(0,1)=Jzk+1​​(0,4)=Jzk+1​​(1,0)=Jzk+1​​(1,4)=Jzk+1​​(2,4)​
根据链式求导法，Jzk+1J_{z_{k+1}}Jzk+1​​可由JzkJ_{z_{k}}Jzk​​（初值为单位阵III）递推得到：
Jzk+1=.........Fi=1i=2Fi=0i=1JzkJ_{z_{k+1}}=......... F^{i=2}_{i=1}F^{i=1}_{i=0}J_{z_{k}} Jzk+1​​=.........Fi=1i=2​Fi=0i=1​Jzk​​

七、VINS代码实践

VINS中关于IMU预积分的代码都集中在integration_base.h中，实现了一个IntegrationBase类。

1.预积分类的数据成员与构造函数

    double dt; //IMU帧的时间间隔Eigen::Vector3d acc_0, gyr_0; //当前帧传入的IMU加速度和角速度Eigen::Vector3d acc_1, gyr_1;//上一帧IMU加速度和角速度const Eigen::Vector3d linearized_acc, linearized_gyr;//当前帧传入的IMU加速度和角速度Eigen::Vector3d linearized_ba, linearized_bg;//上一帧IMU加速度和角速度的baisEigen::Matrix jacobian, covariance;//雅可比矩阵和协方差矩阵Eigen::Matrix step_jacobian;Eigen::Matrix step_V;Eigen::Matrix noise;//噪声矩阵 包括 n_ak n_wk n_ak+1 n_wk+1 n_ba n_bwdouble sum_dt;  //关键帧的时间间隔Eigen::Vector3d delta_p; //位移增量Eigen::Quaterniond delta_q;//旋转增量Eigen::Vector3d delta_v;//速度增量std::vector dt_buf;//关键帧之间的IMU帧时间间隔std::vector acc_buf;//关键帧之间的IMU帧加速度std::vector gyr_buf;//关键帧之间的IMU帧角速度

IntegrationBase(const Eigen::Vector3d &_acc_0, const Eigen::Vector3d &_gyr_0, //预积分开始时（初始时刻）的IMU加速度和角速度const Eigen::Vector3d &_linearized_ba, const Eigen::Vector3d &_linearized_bg) //一次预积分的IMU加速度和角速度的bais（不会改变）: acc_0{_acc_0}, gyr_0{_gyr_0}, linearized_acc{_acc_0}, linearized_gyr{_gyr_0},//利用传入的IMU加速度和角速度给初始时刻和上一时刻的数据赋值linearized_ba{_linearized_ba}, linearized_bg{_linearized_bg}, //预积分的IMU加速度和角速度的bais给数据成员赋值jacobian{Eigen::Matrix::Identity()}, covariance{Eigen::Matrix::Zero()},//预积分雅可比矩阵初值为单位阵，协方差矩阵为0sum_dt{0.0}, delta_p{Eigen::Vector3d::Zero()}, delta_q{Eigen::Quaterniond::Identity()}, delta_v{Eigen::Vector3d::Zero()}//位移、速度、旋转的增量初始化{noise = Eigen::Matrix::Zero();//初始化噪声矩阵noise.block<3, 3>(0, 0) =  (ACC_N * ACC_N) * Eigen::Matrix3d::Identity();noise.block<3, 3>(3, 3) =  (GYR_N * GYR_N) * Eigen::Matrix3d::Identity();noise.block<3, 3>(6, 6) =  (ACC_N * ACC_N) * Eigen::Matrix3d::Identity();noise.block<3, 3>(9, 9) =  (GYR_N * GYR_N) * Eigen::Matrix3d::Identity();noise.block<3, 3>(12, 12) =  (ACC_W * ACC_W) * Eigen::Matrix3d::Identity();noise.block<3, 3>(15, 15) =  (GYR_W * GYR_W) * Eigen::Matrix3d::Identity();
}

2.添加IMU数据

在类的构造函数初始化预积分数据之后，我们基于当前图像关键帧进行IMU预积分操作，所以需要多次添加IMU帧数据，添加函数为push_back。得到每一帧IMU数据之后进行保存并进行传播。

void push_back(double dt, const Eigen::Vector3d &acc, const Eigen::Vector3d &gyr)
{// 相关时间差和传感器数据保留，方便后续repropagatedt_buf.push_back(dt); //IMU帧之间的时间间隔acc_buf.push_back(acc);//当前IMU帧的加速度gyr_buf.push_back(gyr);//当前IMU帧的角速度propagate(dt, acc, gyr);//传播函数 计算预积分并更新协方差矩阵
}

3.根据IMU数据进行预积分

dt = _dt;//IMU帧间隔
acc_1 = _acc_1;//当前帧IMU加速度
gyr_1 = _gyr_1;//当前帧IMU角速度Vector3d result_delta_p;
Quaterniond result_delta_q;
Vector3d result_delta_v;
Vector3d result_linearized_ba;
Vector3d result_linearized_bg;
//定义变量存储预积分结果midPointIntegration(_dt, acc_0, gyr_0, _acc_1, _gyr_1, delta_p, delta_q, delta_v,linearized_ba, linearized_bg,result_delta_p, result_delta_q, result_delta_v,result_linearized_ba, result_linearized_bg, 1);//checkJacobian(_dt, acc_0, gyr_0, acc_1, gyr_1, delta_p, delta_q, delta_v,
//                    linearized_ba, linearized_bg);
//将中值预积分得到的结果进行赋值
delta_p = result_delta_p;
delta_q = result_delta_q;
delta_v = result_delta_v;
linearized_ba = result_linearized_ba;
linearized_bg = result_linearized_bg;
//四元数结果需要归一化
delta_q.normalize();
sum_dt += dt;
//将当前帧IMU数据保存为上一帧
acc_0 = acc_1;
gyr_0 = gyr_1;  

预积分中最主要的函数是midPointIntegration，实现了一次IMU中值预积分：
参数说明：

void midPointIntegration(
double _dt, 
//两帧IMU的时间间隔const Eigen::Vector3d &_acc_0, const Eigen::Vector3d &_gyr_0,//上一帧的IMU数据const Eigen::Vector3d &_acc_1, const Eigen::Vector3d &_gyr_1,//当前帧的IMU数据const Eigen::Vector3d &delta_p, const Eigen::Quaterniond &delta_q, const Eigen::Vector3d &delta_v,//上一IMU帧的位移 速度 旋转的增量  (已知)const Eigen::Vector3d &linearized_ba, const Eigen::Vector3d &linearized_bg,//预积分过程中的IMU bais  (已知，一次预积分过程中不变)Eigen::Vector3d &result_delta_p, Eigen::Quaterniond &result_delta_q, Eigen::Vector3d &result_delta_v,///当前IMU帧的位移 速度 旋转的增量  （待求）Eigen::Vector3d &result_linearized_ba, Eigen::Vector3d &result_linearized_bg, 预积分过程中的IMU bais  (待求 ，直接由linearized_ba、linearized_bg赋值)bool update_jacobian)//是否更新雅可比矩阵

代码细节：

  Vector3d un_acc_0 = delta_q * (_acc_0 - linearized_ba);//根据上一IMU帧的四元数 将上一帧IMU加速度去bais 变换到b_k坐标系下Vector3d un_gyr = 0.5 * (_gyr_0 + _gyr_1) - linearized_bg;//根据上一帧和当前帧IMU角速度计算中值角速度result_delta_q = delta_q * Quaterniond(1, un_gyr(0) * _dt / 2, un_gyr(1) * _dt / 2, un_gyr(2) * _dt / 2);//计算当前帧四元数 旋转角度比较小 \gamma_{k+1} 近似为 [1,\theta /2]Vector3d un_acc_1 = result_delta_q * (_acc_1 - linearized_ba);//根据当前IMU帧的四元数 将当前IMU帧加速度去bais 变换到b_k坐标系下Vector3d un_acc = 0.5 * (un_acc_0 + un_acc_1);//根据上一帧和当前帧IMU加速度（b_k系下）计算中值加速度result_delta_p = delta_p + delta_v * _dt + 0.5 * un_acc * _dt * _dt;//计算位移增量result_delta_v = delta_v + un_acc * _dt;//计算速度增量result_linearized_ba = linearized_ba;result_linearized_bg = linearized_bg;      //两图像关键帧之间的预积分认为bais不变 所以 直接赋值

接下来的代码主要是根据第五节中的离散化公式计算FFF矩阵以及VVV矩阵。为了简化计算过程，作者提前先计算了三个反对称矩阵：(a^k−bak)∧(\hat{a}_k-b_{a_k})^{\wedge}(a^k​−bak​​)∧ 、(a^k+1−bak)∧(\hat{a}_{k+1}-b_{a_{k}})^{\wedge}(a^k+1​−bak​​)∧ 、(w^k+w^k+12−bwk)∧(\frac{\hat{w}_k+\hat{w}_{k+1}}{2}-b_{w_k})^{\wedge}(2w^k​+w^k+1​​−bwk​​)∧

  Vector3d w_x = 0.5 * (_gyr_0 + _gyr_1) - linearized_bg;Vector3d a_0_x = _acc_0 - linearized_ba;Vector3d a_1_x = _acc_1 - linearized_ba;Matrix3d R_w_x, R_a_0_x, R_a_1_x;R_w_x<<0, -w_x(2), w_x(1),w_x(2), 0, -w_x(0),-w_x(1), w_x(0), 0;R_a_0_x<<0, -a_0_x(2), a_0_x(1),a_0_x(2), 0, -a_0_x(0),-a_0_x(1), a_0_x(0), 0;R_a_1_x<<0, -a_1_x(2), a_1_x(1),a_1_x(2), 0, -a_1_x(0),-a_1_x(1), a_1_x(0), 0;

接下来套用公式计算（具体实现见源代码及公式）：

 MatrixXd F = MatrixXd::Zero(15, 15);//略具体赋值 MatrixXd V = MatrixXd::Zero(15,18);//略具体赋值 

值得注意的是，在在计算VVV矩阵时，关于nak、nak+1、nwk+1、nwkn_{a_k} 、 n_{a_{k+1}} 、n_{w_{k+1}} 、n_{w_{k}}nak​​、nak+1​​、nwk+1​​、nwk​​的系数与前面的计算相差一个符号，但是由于是均值为0的高斯白噪声，所以其效果是一样的。

最后每次预积分更新雅可比JJJ和协方差PPP：

jacobian = F * jacobian;
covariance = F * covariance * F.transpose() + V * noise * V.transpose();